题目内容
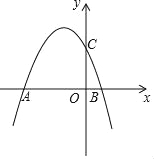
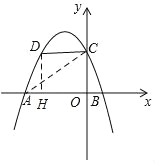
【题目】如图,二次函数y=ax2﹣![]() x+2(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,已知点A(﹣4,0).
x+2(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,已知点A(﹣4,0).
(1)求抛物线与直线AC的函数解析式;
(2)若点D(m,n)是抛物线在第二象限的部分上的一动点,四边形OCDA的面积为S,求S关于m的函数关系;
(3)若点E为抛物线上任意一点,点F为x轴上任意一点,当以A、C、E、F为顶点的四边形是平行四边形时,请直接写出满足条件的所有点E的坐标.
【答案】(1)![]() (2)S=﹣m2﹣4m+4(﹣4<m<0)(3)(﹣3,2)、(
(2)S=﹣m2﹣4m+4(﹣4<m<0)(3)(﹣3,2)、(![]() ,﹣2)、(
,﹣2)、(![]() ,﹣2)
,﹣2)
【解析】
试题分析:(1)把点A的坐标代入抛物线的解析式,就可求得抛物线的解析式,根据A,C两点的坐标,可求得直线AC的函数解析式;
(2)先过点D作DH⊥x轴于点H,运用割补法即可得到:四边形OCDA的面积=△ADH的面积+四边形OCDH的面积,据此列式计算化简就可求得S关于m的函数关系;
(3)由于AC确定,可分AC是平行四边形的边和对角线两种情况讨论,得到点E与点C的纵坐标之间的关系,然后代入抛物线的解析式,就可得到满足条件的所有点E的坐标.
试题解析:(1)∵A(﹣4,0)在二次函数y=ax2﹣![]() x+2(a≠0)的图象上,
x+2(a≠0)的图象上,
∴0=16a+6+2,
解得a=﹣![]() ,
,
∴抛物线的函数解析式为y=﹣![]() x2﹣
x2﹣![]() x+2;
x+2;
∴点C的坐标为(0,2),
设直线AC的解析式为y=kx+b,则
![]() ,
,
解得![]() ,
,
∴直线AC的函数解析式为:![]() ;
;
(2)∵点D(m,n)是抛物线在第二象限的部分上的一动点,
∴D(m,﹣![]() m2﹣
m2﹣![]() m+2),
m+2),
过点D作DH⊥x轴于点H,则DH=﹣![]() m2﹣
m2﹣![]() m+2,AH=m+4,HO=﹣m,
m+2,AH=m+4,HO=﹣m,
∵四边形OCDA的面积=△ADH的面积+四边形OCDH的面积,
∴S=![]() (m+4)×(﹣
(m+4)×(﹣![]() m2﹣
m2﹣![]() m+2)+
m+2)+![]() (﹣
(﹣![]() m2﹣
m2﹣![]() m+2+2)×(﹣m),
m+2+2)×(﹣m),
化简,得S=﹣m2﹣4m+4(﹣4<m<0);
(3)①若AC为平行四边形的一边,则C、E到AF的距离相等,
∴|yE|=|yC|=2,
∴yE=±2.
当yE=2时,解方程﹣![]() x2﹣
x2﹣![]() x+2=2得,
x+2=2得,
x1=0,x2=﹣3,
∴点E的坐标为(﹣3,2);
当yE=﹣2时,解方程﹣![]() x2﹣
x2﹣![]() x+2=﹣2得,
x+2=﹣2得,
x1=![]() ,x2=
,x2=![]() ,
,
∴点E的坐标为(![]() ,﹣2)或(
,﹣2)或(![]() ,﹣2);
,﹣2);
②若AC为平行四边形的一条对角线,则CE∥AF,
∴yE=yC=2,
∴点E的坐标为(﹣3,2).
综上所述,满足条件的点E的坐标为(﹣3,2)、(![]() ,﹣2)、(
,﹣2)、(![]() ,﹣2).
,﹣2).

 名校课堂系列答案
名校课堂系列答案