题目内容
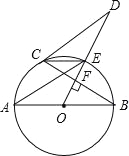
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则sin∠BOE的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】由题意可知,OE为对角线AC的中垂线,则CE=AE=5,S△AEC=2S△AOE=10,由S△AEC求出线段AE的长度,进而在Rt△BCE中,由勾股定理求出线段BE的长度;然后证明∠BOE=∠BCE,从而可求得结果.
解:如图所示,连接EC.
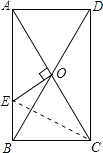
由题意可得,OE为对角线AC的垂直平分线,
∴CE=AE,S△AOE=S△COE=5,
∴S△AEC=2S△AOE=10.
∴![]() AEBC=10,又BC=4,
AEBC=10,又BC=4,
∴AE=5,
∴EC=5.
在Rt△BCE中,由勾股定理得:BE=![]() =3.
=3.
∵∠EBC+∠EOC=90°+90°=180°,
∴B、C、O、E四点共圆,
∴∠BOE=∠BCE.
(另解:∵∠AEO+∠EAO=90°,∠AEO=∠BOE+∠ABO,
∴∠BOE+∠ABO+∠EAO=90°,又∠ABO=90°-∠OBC=90°-(∠BCE+∠ECO)
∴∠BOE+(90°-(∠BCE+∠ECO))+∠EAO=90°,
化简得:∠BOE-∠BCE-∠ECO+∠EAO=0
∵OE为AC中垂线,
∴∠EAO=∠ECO.
代入上式得:∠BOE=∠BCE.)
∴sin∠BOE=sin∠BCE=![]() .
.
故答案为: ![]() .
.
“点睛”本题是几何综合题,考查了矩形性质、线段垂直平分线的性质、勾股定理、圆周角、三角函数的定义等知识点,有一定的难度.解题要点有两个:(1)求出线段AE的长度;(2)证明∠BOE=∠BCE.

练习册系列答案
相关题目