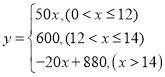题目内容
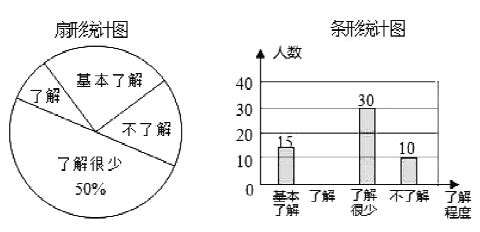
【题目】某校九年级有 ![]() 名学生,在体育考试前随机抽取部分学生进行跳绳测试,根据测试成绩制作了下面两个不完整的统计图.请根据相关信息,解答下列问题:
名学生,在体育考试前随机抽取部分学生进行跳绳测试,根据测试成绩制作了下面两个不完整的统计图.请根据相关信息,解答下列问题:
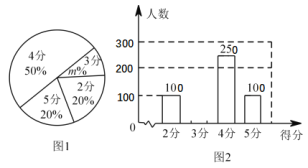
(1)本次参加跳绳测试的学生人数为 ,图 ![]() 中
中 ![]() 的值为 ;
的值为 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校九年级跳绳测试中得 ![]() 分的学生约有多少人?
分的学生约有多少人?
【答案】(1)500,10;(2)平均数是: 3.7分,众数是:4分;中位数是:4分;(3)150人.
【解析】
(1)根据得2分的人数和所占的百分比求出总人数,再用3分的人数除以总人数,即可得出m的值;
(2)利用加权平均数公式求得平均数,然后利用众数、中位数定义求解即可;
(3)利用总人数乘以对应的百分比即可求解.
(1)本次参加跳绳测试的学生人数为100÷20%=500(人),
m%=![]() ×100%=10%,即m=10;
×100%=10%,即m=10;
故答案为:500,10;
(2)3分的人数有500-100-250-100=50人,
平均数是:![]() (100×2+50×3+250×4+100×5)=3.7(分),
(100×2+50×3+250×4+100×5)=3.7(分),
∵4分出现的次数最多,出现了250次,
∴众数是:4分;
把这些数从小到大排列,则中位数是:4分;
(3)该校九年级跳绳测试中得3分的学生约有:1500×10%=150(人).

【题目】某通讯经营店销售![]() ,
,![]() 两种品牌儿童手机,今年进货和销售价格如下表:
两种品牌儿童手机,今年进货和销售价格如下表:
|
| |
进货价格(元/只) | 1000 | 1100 |
销售价格(元/只) |
| 1500 |
已知![]() 型手机去年4月份销售总额为3.6万元,今年经过改造升级后每部销售价比去年增加400元.今年4月份
型手机去年4月份销售总额为3.6万元,今年经过改造升级后每部销售价比去年增加400元.今年4月份![]() 型手机的销售数量与去年4月份相同,而销售总额为5.4万元.
型手机的销售数量与去年4月份相同,而销售总额为5.4万元.
(1)求今年4月份![]() 型手机的销售价是多少元?
型手机的销售价是多少元?
(2)该店计划6月份再进一批![]() 型和
型和![]() 型手机共50部且
型手机共50部且![]() 型手机数量不超过
型手机数量不超过![]() 型手机数量的2倍,应如何进货才能使这批儿童手机获利最多?
型手机数量的2倍,应如何进货才能使这批儿童手机获利最多?
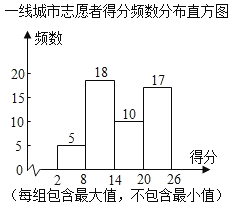
【题目】为了解疫情对精神负荷造成的影响,某机构分别在一线城市和三线城市的志愿者中随机选取了50人参加LES测试,根据志愿者的答题情况计算出LES得分,并对得分进行整理,描述和分析,部分信息如下:
一、三线城市志愿者得分统计表
城市 | 中位数 | 平均数 |
一线城市 | a | 17.6 |
三线城市 | 14 | 17.2 |
注:一线城市在14<x≤20中的得分是:15,15,16,17,17,17,17,18,18,20.
根据以上信息,解答下列问题:
(1)表中a的值为 ;
(2)得分越低反映个体承受的精神压力越小,排名越靠前,在这次调查中,一线城市的志愿者甲和三线城市的志愿者乙的得分均为15分,请判断甲、乙在各自城市选取的志愿者中得分排名谁更靠前,并说明理由;
(3)如果得分超过平均数就需要进行心理干预,请估计一线城市全部2000名志愿者中有多少人需要进行心理干预?