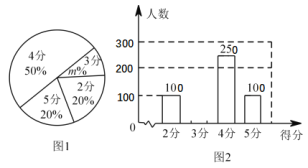
ΧβΡΩΡΎ»ί
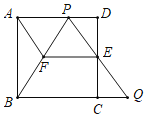
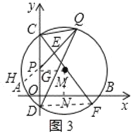
ΓΨΧβΡΩΓΩ»γΆΦ1Θ°“―÷ΣΓ―M”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ§”κy÷αΫΜ”ΎCΓΔDΝΫΒψΘ§AΓΔBΝΫΒψΒΡΚαΉχ±ξΖ÷±πΈΣ©¹1ΚΆ7Θ§œ“ABΒΡœ“–ΡΨύMNΈΣ3Θ§
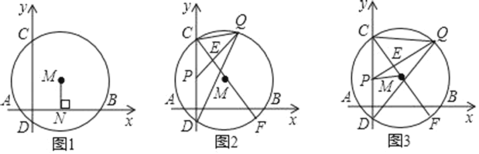
Θ®1Θ©«σΓ―MΒΡΑκΨΕΘΜ
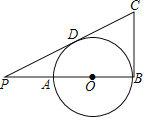
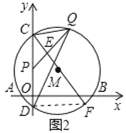
Θ®2Θ©»γΆΦ2Θ§P‘Ύœ“CD…œΘ§«“CPΘΫ2Θ§Q «ΜΓBC…œ“ΜΕ·ΒψΘ§PQΫΜ÷±ΨΕCF”ΎΒψEΘ§Β±ΓœCPQΘΫΓœCQD ±Θ§
ΔΌ≈–ΕœœΏΕΈPQ”κ÷±ΨΕCFΒΡΈΜ÷ΟΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
ΔΎ«σCQΒΡ≥ΛΘΜ
Θ®3Θ©»γΆΦ3Θ°»τPΒψ «œ“CD…œ“ΜΕ·ΒψΘ§Q «ΜΓBC…œ“ΜΕ·ΒψΘ§PQΫΜ÷±ΨΕCF”ΎΒψEΘ§Β±ΓœCPQ”κΓœCQDΜΞ”ύ ±Θ§«σΓςPEMΟφΜΐΒΡΉν¥σ÷ΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©5ΘΜΘ®2Θ©ΔΌPQΓΆCFΘΜœξΦϊΫβΈωΘΜΔΎ4ΘΜΘ®3Θ©ΓςPEMΟφΜΐΒΡΉν¥σ÷ΒΈΣ3
ΓΨΫβΈωΓΩ
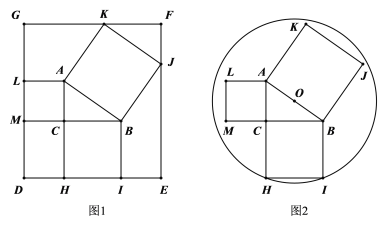
Θ®1Θ©Ν§Ϋ”MBΘ§ΗυΨίΧβ“βΒΟ≥ωAB=8Θ§‘ΌΫαΚœ¥ΙΨΕΕ®άμΩ…ΒΟBN=4Θ§ΉνΚσΫχ“Μ≤Ϋάϊ”ΟΙ¥Ι…Ε®άμΦΤΥψ«σΫβΦ¥Ω…ΘΜ
Θ®2Θ©ΔΌΝ§Ϋ”DFΘ§”…‘≤÷ήΫ«Ε®άμΒΟ≥ωΓœCDF=90ΓψΘ§”…¥ΥΫχ“Μ≤Ϋ÷ΛΟςΓœCEPΘΫ90ΓψΦ¥Ω…ΘΜΔΎΉςMNΓΆAB”ΎNΘ§MGΓΆCD”ΎGΘ§―”≥ΛQPΫΜΓ―M”ΎHΘ§¥”ΕχΆ®ΙΐΖ÷ΈωΩ…ΒΟAN=4Θ§MN=3,MG=ON=3Θ§‘Ό’ΏΒΟ≥ωMN=MGΘ§Ϋχ“Μ≤Ϋ÷ΛΟςCD=AB=8Θ§»ΜΚσάϊ”ΟΙ¥Ι…Ε®άμ«σΒΟDF=6Θ§Ϋ”Ή≈÷ΛΟςΓςCPE”κΓςCFDœύΥΤΘ§άϊ”ΟœύΥΤ»ΐΫ«–Έ–‘÷ ΒΟ≥ωCE”κPEΒΡ≥ΛΘ§¥”Εχ«σ≥ωEFΘ§ΉνΚσ‘Ύ¥ΥΜυ¥Γ…œΫχ“Μ≤ΫΖ÷Έω«σΫβΦ¥Ω…ΘΜ
Θ®3Θ©œ»÷Λ≥ωΓœDCF=ΓœCPQΘ§ΒΟ≥ωCE=PEΘ§‘ΌΉςEKΓΆCP”ΎKΘ§PTΓΆCM”ΎTΘ§Ν§Ϋ”DFΘ§‘ρCKΘΫPKΘ§![]() Θ§Ψί¥Υ…ηEKΘΫ3xΘ§‘ρCKΘΫ4xΘ§CEΘΫPEΘΫ5xΘ§PCΘΫ8xΘ§Ϋ”Ή≈÷ΛΟςΓςCPT~ΓςCFDΘ§άϊ”ΟœύΥΤ»ΐΫ«–Έ–‘÷ ΒΟ≥ωPTΘΫ
Θ§Ψί¥Υ…ηEKΘΫ3xΘ§‘ρCKΘΫ4xΘ§CEΘΫPEΘΫ5xΘ§PCΘΫ8xΘ§Ϋ”Ή≈÷ΛΟςΓςCPT~ΓςCFDΘ§άϊ”ΟœύΥΤ»ΐΫ«–Έ–‘÷ ΒΟ≥ωPTΘΫ![]() Θ§CTΘΫ
Θ§CTΘΫ![]() Θ§ΉνΚσΗυΨί»ΐΫ«–ΈΟφΜΐΙΪ ΫΒΟΒΫΓςPEMΒΡΟφΜΐ
Θ§ΉνΚσΗυΨί»ΐΫ«–ΈΟφΜΐΙΪ ΫΒΟΒΫΓςPEMΒΡΟφΜΐ![]() Θ§”…¥Υάϊ”ΟΕΰ¥ΈΚ· ΐΒΡ–‘÷ Ϋχ“Μ≤Ϋ«σΫβΦ¥Ω….
Θ§”…¥Υάϊ”ΟΕΰ¥ΈΚ· ΐΒΡ–‘÷ Ϋχ“Μ≤Ϋ«σΫβΦ¥Ω….
Θ®1Θ©Ν§Ϋ”MBΘ§»γΆΦ1Υυ ΨΘΚ

ΓΏAΓΔBΝΫΒψΒΡΚαΉχ±ξΖ÷±πΈΣ![]() ΚΆ7Θ§
ΚΆ7Θ§
ΓύABΘΫ8Θ§
ÿMNâABȧ
ΓύBNΘΫ4Θ§
‘ΎRtΓςBMN÷–Θ§”…Ι¥Ι…Ε®άμΒΟΘΚ
![]() Θ§
Θ§
ΓύΓ―MΒΡΑκΨΕΈΣ5ΘΜ
Θ®2Θ©ΔΌPQΓΆCFΘΜάμ”…»γœ¬ΘΚ
Ν§Ϋ”DFΘ§»γΆΦ2Υυ ΨΘ§
ΓΏCF «Γ―MΒΡ÷±ΨΕΘ§
ΓύΓœCDFΘΫ90ΓψΘ§
ΓύΓœCFD+ΓœDCFΘΫ90ΓψΘ§
ΓΏΓœCQDΘΫΓœCFDΘ§
ΓύΓœCQD+ΓœDCFΘΫ90ΓψΘ§
ΓΏΓœCPQΘΫΓœCQDΘ§
ΓύΓœCPQ+ΓœDCFΘΫ90ΓψΘ§
ΓύΓœCEPΘΫ90ΓψΘ§
ΓύPQΓΆCFΘΜ
ΔΎΉςMNΓΆAB”ΎNΘ§MGΓΆCD”ΎGΘ§―”≥ΛQPΫΜΓ―M”ΎHΘ§»γΆΦ3Υυ ΨΘΚ
‘ρANΘΫ4Θ§MNΘΫ3Θ§MGΘΫONΘΫ3Θ§
ΓύMNΘΫMGΘ§
ΓύCDΘΫABΘΫ8Θ§
‘ΎRtΓςCDF÷–Θ§CFΘΫ2BMΘΫ10Θ§![]() Θ§
Θ§
”…ΔΌΒΟΘΚPQΓΆCFΘ§
ΓύΓœCEPΘΫΓœCDFΘΫ90ΓψΘ§EHΘΫEQΘ§
ΓΏΓœPCEΘΫΓœFCDΘ§
ΓύΓςCPE~ΓςCFDΘ§
Γύ![]() Θ§
Θ§
Φ¥![]() Θ§
Θ§
ΫβΒΟΘΚCEΘΫ![]() Θ§PEΘΫ
Θ§PEΘΫ![]() Θ§
Θ§
ΓύEFΘΫCFCEΘΫ![]() Θ§
Θ§
ΓΏEQΓΝEHΘΫCEΓΝEFΘ§Φ¥![]() Θ§
Θ§
‘ΎRtΓςCPE÷–Θ§”…Ι¥Ι…Ε®άμΒΟΘΚ![]() ΘΜ
ΘΜ
Θ®3Θ©ΓΏCF «Γ―MΒΡ÷±ΨΕΘ§
ΓύΓœCDFΘΫ90ΓψΘ§
ΓύΓœF+ΓœDCFΘΫ90ΓψΘ§
ΓΏΓœCQDΘΫΓœFΘ§
ΓύΓœCQD+ΓœDCFΘΫ90ΓψΘ§
ΓΏΓœCPQ+ΓœCQDΘΫ90ΓψΘ§
ΓύΓœDCFΘΫΓœCPQΘ§
ΓύCEΘΫPEΘ§
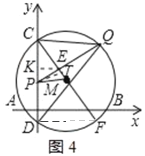
ΉςEKΓΆCP”ΎKΘ§PTΓΆCM”ΎTΘ§‘ΌΝ§Ϋ”DFΘ§»γΆΦ4Υυ ΨΘ§
‘ρCKΘΫPKΘ§![]() Θ§
Θ§
…ηEKΘΫ3xΘ§‘ρCKΘΫ4xΘ§CEΘΫPEΘΫ5xΘ§PCΘΫ8xΘ§
ΓΏΓœPCT=ΓœDCFΘ§ΓœCTP=ΓœCDF=90ΓψΘ§
ΓύΓςCPT~ΓςCFDΘ§
Γύ![]() Θ§
Θ§
ΓύPTΘΫ![]() Θ§CTΘΫ
Θ§CTΘΫ![]() Θ§
Θ§
ΓύΓςPEMΒΡΟφΜΐ![]() Θ§
Θ§
ΓΏ![]() Θ§
Θ§
ΓύS”–Ήν¥σ÷ΒΘ§«“Β±![]() ±Θ§SΒΡΉν¥σ÷ΒΈΣ3Θ§
±Θ§SΒΡΉν¥σ÷ΒΈΣ3Θ§
Φ¥ΓςPEMΟφΜΐΒΡΉν¥σ÷ΒΈΣ3Θ°