Question

【题目】二次函数图象轴上方的部分沿轴翻折到轴下方，图象的其余部分保持不变，翻折后的图象与原图象轴下方的部分组成一个“”形状的新图象，若直线与该新图象有两个公共点，则的取值范围为_____.

Answer 1

【答案】或

【解析】

画出图象求出直线经过点A和原点时的b的值，结合图象可以确定b的范围，再求出直线与翻折后的抛物线只有一个交点时的b的值，可以利用方程组只有一组解△=0解决问题，由此再确定b的取值范围．

如图,

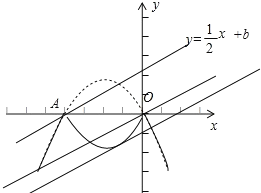
当直线经过点A(2,0)时，b=1，

当直线经过点O(0,0)时，b=0，

∴0<b<1时,直线与新图形有两个交点，

翻折后的抛物线为

由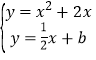方程组有一组解,消去y得到：2x2+3x2b=0，

∵△=0，

∴9+16b=0，

由图象可知,时,直线与新图形有两个交点.

综上所述0<b<1或时,直线与新图形有两个交点.

故答案为：或.