Question

【题目】四边形ABCD中，BD是对角线，∠ABC=90°，tan∠ABD=，AB=20，BC=10，AD=13，则线段CD=__．

Answer 1

【答案】17

【解析】

作AH⊥BD于H，CG⊥BD于G，根据正切的定义分别求出AH、BH，根据勾股定理求出HD，得到BD，根据勾股定理计算即可．

当∠ADB为锐角时，作AH⊥BD于H，CG⊥BD于G，

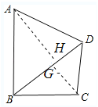
∵tan∠ABD= ，

∴ =，

设AH=3x，则BH=4x，

由勾股定理得，（3x）2+（4x）2=202，

解得，x=4，

则AH=12，BH=16，

在Rt△AHD中，HD==5，

∴BD=BH+HD=21，

∵∠ABD+∠CBD=90°，∠BCH+∠CBD=90°，

∴∠ABD=∠CBH，

∴ =，又BC=10，

∴BG=6，CG=8，

∴DG=BD﹣BG=15，

∴CD==17，

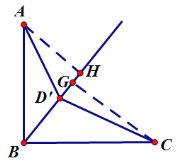
当∠ADB为钝角时，由勾股定理得BH=16,BG=6,GH=BH-BG=10,

在△A D′H中，由勾股定理得

D′H=5，

∵D′H＜GH，∴此种情况不存在.

故答案为：17