��Ŀ����
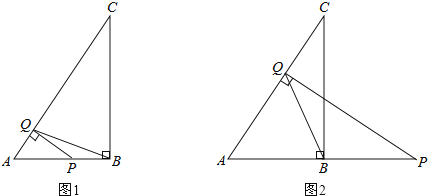
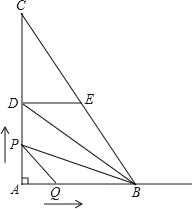
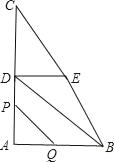
����Ŀ����ͼ����ֱ����ABC�У���A��90����AB��6��AC��8��D��E�ֱ���AC��BC�ߵ��е㣬��P��A�������߶�AD��DE��EB��ÿ��3����λ�����ٶ���B�����˶�����Q�ӵ�A����������AB��ÿ��2����λ�����ٶ������˶�������P���B�غ�ʱֹͣ�˶�����QҲ��ֹ֮ͣ�˶������P��Q�˶�ʱ����t�룬��t��0��
��1����t���� ��ʱ����P�����յ�B��
��2������P�˶�����Dʱ������BPQ�������
��3������BPQ�����ΪS�������Q���߶�AB���˶�ʱ��S��t�ĺ�����ϵʽ��
��4����ֱ��д��PQ��DBʱt��ֵ��
���𰸡���1��4�룻��2��![]() ����3��Q���߶�AB���˶�ʱ��S��t�ĺ�����ϵʽΪS��
����3��Q���߶�AB���˶�ʱ��S��t�ĺ�����ϵʽΪS��![]() ����4��
����4��![]()
��������
��1������֪���ɶ��������BC������D��E�ֱ���AC��BC���е㣬���AD��DE��BE���Ӷ����t��
��2�����������P�˶�����Dʱ����ʱ�䣬�ó�AQ�ij����������BQ�ij����ٸ�����BPQ�����=![]() BQAP���м��㼴�ɣ�
BQAP���м��㼴�ɣ�
��3������֪��t��ʾ��AQ��AP��BQ�����ɡ�A=90����ͨ�������ʽ���S��t�ĺ�����ϵʽ��
��4��ͨ�����裬������������ۼ�����⣮
��1����֪Rt��ABC�У���A��90�㣬AB��6��AC��8��
�ɹ��ɶ����ã�BC��![]() ��
��![]() ��10��
��10��
����D��E�ֱ���AC��BC���е㣬
��AD��4��DE��3��BE��5��
�൱��P�����յ�Bʱ����ʱ��t����4+3+5����3��4���룩��
��t��ֵΪ4�룮
��2������P�˶�����Dʱ������ʱ��Ϊ![]() �룬
�룬
����AQ��![]() ��2��
��2��![]() ��
��
��BQ��6��![]() ��
��![]() ��
��
���BPQ�������![]() BQAP��
BQAP��![]() ��4��
��4��![]() ��
��
��3������ͼ������P��AD�ϣ�������D�㣩��
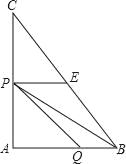
����֪�ã�AQ��2t��AP��3t��
��BQ��AB��AQ��6��2t��
��֪��A��90�㣬
���BPQ�����S��![]() BQAP��
BQAP��![]() ��6��2t��3t����3t2+9t��
��6��2t��3t����3t2+9t��
����Q���߶�AB���˶�ʱ��S��t�ĺ�����ϵʽΪS����3t2+9t��
����ͼ����P��DE��������D��E���ϣ�
����P��PF��AB��F��
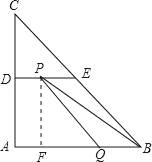
��PF��AD��4��
���BPQ�����S��![]() BQPF��
BQPF��![]() ��6��2t��4��12��4t��
��6��2t��4��12��4t��
���Դ�ʱQ���߶�AB���˶�ʱ��S��t�ĺ�����ϵʽΪS��12��4t��
�۵���P��BE�ϣ�������E�㣩��
����֪�ã�BP��3+4+5��3t��12��3t��
����P��PF��AB��F��
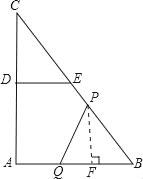
��PF��AC��
���BPF�ס�BCA��
��![]() ��
��
��![]() ��
��
��PF��![]() ��
��
���BPQ�����S��![]() BQPF��
BQPF��![]() ��6��2t��
��6��2t��![]() ��
��![]() ����
����
����Q���߶�AB���˶�ʱ��S��t�ĺ�����ϵʽΪS��![]() ����
����
��4����PQ��DB�����P��Q����DBͬ�࣮�����������
�ٵ���Q��AB�ϣ���P��AD��ʱ��
����PQ��DB������
���AQP�ס�ABD��
��![]() ��
��
��![]() ��
��
��ʱ���̵Ľ���t��0�����˽ⲻ�������⣬
��PQ��DB��������
�ڵ�3��t��4ʱ����Q��AB�ӳ����ϣ���P��EB�ϣ�

��ʱPB��12��3t��PE��3t��7��BQ��2t��6��
��PQ��DB����ֱ��PQ��DE��N��
��DE��AB��
���PEN�ס�PBQ��
��EN��BQ��PE��PB��
��EN��![]() ��
��
�֡�NQ��DB��
��EN��ED��EP��EB��
��EN��![]() ��
��
����![]() ��
��![]() ��
��
���t��![]() �������⣮
�������⣮
������������t��![]() ʱ��PQ��DB��
ʱ��PQ��DB��