题目内容
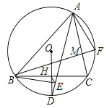
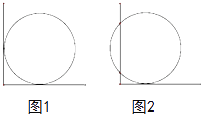
【题目】如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;(2)如图3,如果α=45°,AB=2,AE=4![]() ,求点G到BE的距离.
,求点G到BE的距离.
【答案】(1)证明见解析;(2)点G到BE的距离为![]() .
.
【解析】
(1)由旋转的性质得到∠BAE=∠DAG,由正方形的性质得到AB=AD,AE=AG,然后依据SAS可证明△ABE≌△ADG,然后依据全等三角形的性质进行证明即可;
(2)连接GE、BG,延长AD交GE与H.当α=45°时,可证明△AHE为等腰直角三角形,然后可求得AH和HE的长,然后依据等腰三角形三线合一的性质可得到EG=2HE,最后在△BEG中,利用面积法可求得点G到BE的距离.
(1)由旋转的性质可知:∠BAE=∠DAG,由正方形的性质可知:AB=AD,AE=AG.
∵在△ABE和△ADG中,
∴△ABE≌△ADG.
∴BE=DG.
(2)连接GE、BG,延长AD交GE与H.
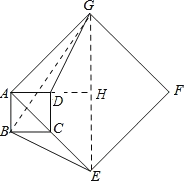
当![]() 时,则
时,则![]()
∵![]()
∴![]()
又∵AE=AG,
∴AH⊥GE.
又∵AH⊥AB,![]()
∴△AHE为等腰直角三角形,
∴![]()
∴EG=2EH=8.
∴![]()
设点G到BE的距离为h. ![]()
![]() 即
即![]() ,解得
,解得![]()
∴点G到BE的距离为![]()

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案【题目】为降低空气污染,公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年均载客量如表:
A型 | B型 | |
价格(万元/辆) | a | b |
年均载客量(万人/年/辆) | 60 | 100 |
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元
(1)求购买每辆A型公交车和每辆B型公交车分别多少万元?
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车年均载客总和不少于680万人次,有哪几种购车方案?请你设计一个方案,使得购车总费用最少.