Question

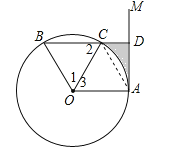
【题目】如图，点A是直线AM与⊙O的交点，点B在⊙O上，BD⊥AM垂足为D，BD与⊙O交于点C，OC平分∠AOB，∠B=60°．

（1）求证：AM是⊙O的切线；

（2）若DC=2，求图中阴影部分的面积．（结果保留π和根号）

Answer 1

【答案】（1）答案见解析；（2）．

【解析】试题分析：（1）由已知条件得到△BOC是等边三角形，根据等边三角形的性质得到∠1=∠2=60°，由角平分线的性质得到∠1=∠3，根据平行线的性质得到∠OAM=90°，于是得到结论；

（2）根据等边三角形的性质得到∠OAC=60°，根据三角形的内角和得到∠CAD=30°，根据勾股定理得到AD的长，于是得到结论．

（1）∵∠B=60°，∴△BOC是等边三角形，∴∠1=∠2=60°，∵OC平分∠AOB，∴∠1=∠3，∴∠2=∠3，∴OA∥BD，∴∠BDM=90°，∴∠OAM=90°，∴AM是⊙O的切线；

（2）∵∠3=60°，OA=OC，∴△AOC是等边三角形，∴∠OAC=60°，∵∠OAM=90°，∴∠CAD=30°，∵CD=2，∴AC=2CD=4，∴AD=，∴S阴影=S梯形OADC﹣S扇形OAC=（4+2）×﹣ =．