��Ŀ����
����Ŀ����ѧ����ϣ�ͬѧ��̽���˽�ƽ���ߵ������������������ͬѧ��������
�������
��ͼ����AOB��һ������ǣ��ڱ�OA��OB�Ϸֱ�ȡOM��ON���ٹ���O��MN�Ĵ��ߣ�����ΪP��������OP���ǡ�AOB��ƽ���ߣ�

С�������� ��ͼ����AOB��һ������ǣ��ڱ�OA��OB�Ϸֱ�ȡOM=ON���ƶ��dzߣ�ʹ�dz�������ͬ�Ŀ̶ȷֱ���M��N�غϣ����dz߶���C������OC���ǡ�AOB��ƽ���ߣ�
|
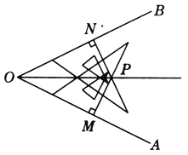
С�յ����� ��ͼ����AOB��һ������ǣ��ڱ�OA��OB�Ϸֱ�ȡOM��ON���ٷֱ����M��N��OA��OB�Ĵ��ߣ�����ΪP��������OP���ǡ�AOB��ƽ���ߣ�
|
����������龳�������������
(1)������������� ��
(2)Ϊ˵��С����������ȷ�ģ�����������֤�����̣�
֤������OM��ON��OC��OC�� ��
���OMC�ա�ONC( )(������������)
(3)С�յ�������ȷ��?��˵������
���𰸡���1���������������ߺ�һ��������2��CM=CN���߱߱ߣ���3����ȷ��֤������⣮
��������
��1�����õ������������ߺ�һ���������ɵõ����۳�����
��2������SSS������֤����OMC�ա�ONC����ȫ�������ɣ�
��3������HL������֤��Rt��OPM��Rt��OPN�����ɵõ����۳�����
�⣺��1����OM=ON��
���OMN�ǵ��������Σ�
��OP��MN��
��OP�ǵױ��ϵĸߣ�Ҳ�ǵױ��ϵ����ߣ�Ҳ�ǡ�MON�Ľ�ƽ���ߣ�
�ʴ�Ϊ���������������ߺ�һ������
��2��֤������OM��ON��OC��OC��CM=CN��
���OMC�ա�ONC���߱߱ߣ���
���MOC=��NOC��
��OCƽ�֡�AOB��
�ʴ�Ϊ��CM=CN���߱߱ߣ�
��3��С�յ�������ȷ��֤�����£�
��PM��OA��PN��OB��
���OMP=��ONP=90�㣬
��OM=ON��OP=OP��
��Rt��OPM��Rt��OPN��HL����
���MOP=��NOP��
��OPƽ�֡�AOB��
![]() С�յ�������ȷ��
С�յ�������ȷ��