Question

【题目】我们知道平行四边形有很多性质，现在如果我们把平行四边形沿着它的一条对角线翻折，会发现这其中还有更多的结论.

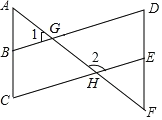
（发现与证明）中，，将沿翻折至，连结.

结论1：与重叠部分的图形是等腰三角形；

结论2：.

试证明以上结论.

（应用与探究）

在中，已知，，将沿翻折至，连结.若以、、、为顶点的四边形是正方形，求的长.（要求画出图形）

Answer 1

【答案】【发现与证明】结论1：见解析，结论2：见解析；【应用与探究】AC的长为或2.

【解析】

【发现与证明】由平行四边形的性质得出∠EAC=∠ACB，由翻折的性质得出∠ACB=∠ACB′，证出∠EAC=∠ACB′，得出AE=CE；得出DE=B′E，证出∠CB′D=∠B′DA= （180°-∠B′ED），由∠AEC=∠B′ED，得出∠ACB′=∠CB′D，即可得出B′D∥AC；

【应用与探究】：分两种情况：①由正方形的性质得出∠CAB′=90°，得出∠BAC=90°，再由三角函数即可求出AC；②由正方形的性质和已知条件得出AC=BC=2．

【发现与证明】:∵四边形ABCD是平行四边形，

∴AD=BC,AD∥BC，

∴∠EAC=∠ACB，

∵△ABC≌△AB′C，

∴∠ACB=∠ACB′,BC=B′C，

∴∠EAC=∠ACB′，

∴AE=CE，

即△ACE是等腰三角形；

∴DE=B′E，

∴∠CB′D=∠B′DA=12(180°∠B′ED)，

∵∠AEC=∠B′ED，

∴∠ACB′=∠CB′D，

∴B′D∥AC；

【应用与探究】:分两种情况：①如图1所示：

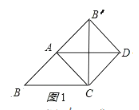
∵四边形ACDB′是正方形，

∴∠CAB′=90°，

∴∠BAC=90°，

∵∠B=45°，

∴AC=；

②如图2所示：AC=BC=2；

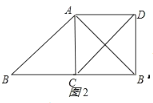
综上所述：AC的长为或2.