题目内容
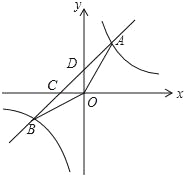
【题目】如图,在平面直角坐标系中,一次函数y=2x-5的图象经过正方形OABC的顶点A和C,则正方形OABC的面积为( )

A.9B.10C.12D.13
【答案】B
【解析】
过点C作CM⊥x轴于点M,过点A做AN⊥y轴于点N,易得△OCM≌△OAN,得到CM=AN,OM=ON;设点C坐标(a,b),可求得A(2a-5,-a),则a=3,可求OC=![]() ,
,
所以正方形面积是10.
解:过点C作CM⊥x轴于点M,过点A做AN⊥y轴于点N,
∵∠COM+∠MOA=∠MOA+∠NOA=90°,
∴∠NOA=∠COM,
又因为OA=OC,
∴Rt△OCM≌Rt△OAN(ASA),
∴OM=ON,CM=AN,
设点C (a,b),
∵点C在函数y=2x-5的图象上,
∴b=2a-5,
∴CM=AN=2a-5,OM=ON=a,
∴A(2a-5,-a),
∴-a=2(2a-5)-5,
∴a=3,
∴C(3,1),
在直角三角形OCM中,由勾股定理可求得OA=![]()
∴正方形OABC的面积是10,
故选B.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
价格/类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
售价(元/盏) | 60 | 100 |
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?