题目内容
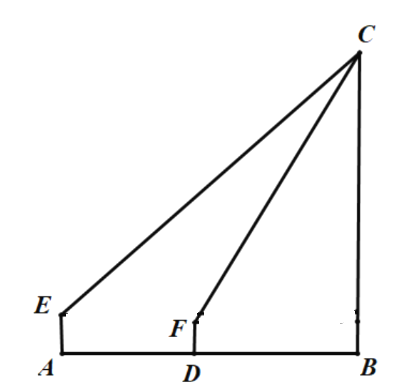
【题目】如图,矩形![]() 的周长是
的周长是![]() ,且
,且![]() 比
比![]() 长
长![]() .若点
.若点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 方向匀速运动,同时点
方向匀速运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 方向匀速运动,当一个点到达点
方向匀速运动,当一个点到达点![]() 时,另一个点也随之停止运动.若设运动时间为
时,另一个点也随之停止运动.若设运动时间为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 之间的函数图象大致是( )
之间的函数图象大致是( )
A.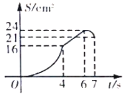 B.
B.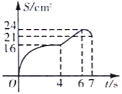
C.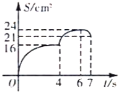 D.
D.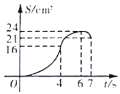
【答案】A
【解析】
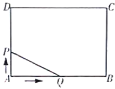
先根据条件求出AB、AD的长,当0≤t≤4时,Q在边AB上,P在边AD上,如图1,计算S与t的关系式,分析图像可排除选项B、C;当4<t≤6时,Q在边BC上,P在边AD上,如图2,计算S与t的关系式,分析图像即可排除选项D,从而得结论.
解:由题意得![]() ,
,![]() ,
,
可解得![]() ,
,![]() ,即
,即![]() ,
,
①当0≤t≤4时,Q在边AB上,P在边AD上,如图1,
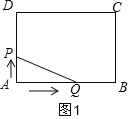
S△APQ=![]() ,
,
图像是开口向上的抛物线,故选项B、C不正确;
②当4<t≤6时,Q在边BC上,P在边AD上,如图2,
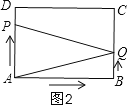
S△APQ=![]() ,
,
图像是一条线段,故选项D不正确;
故选:A.

练习册系列答案
相关题目
【题目】有这样一个问题:探究函数y![]() x的图象与性质.
x的图象与性质.
小亮根据学习函数的经验,对函数y![]() x的图象与性质进行了探究.
x的图象与性质进行了探究.
下面是小亮的探究过程,请补充完整:
(1)函数y![]() x中自变量x的取值范围是 ;
x中自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | 0 | 1 |
|
|
|
| 3 | 4 | 5 | 6 | … |
y | … |
|
|
| 0 |
|
|
|
| m |
|
|
| … |
求m的值;
(3)在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
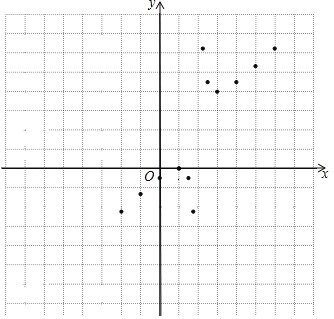
(4)根据画出的函数图象,发现下列特征:
①该函数的图象是中心对称图形,对称中心的坐标是 ;
②该函数的图象与过点(2,0)且平行于y轴的直线越来越靠近而永不相交,该函数的图象还与直线 越来越靠近而永不相交.