题目内容
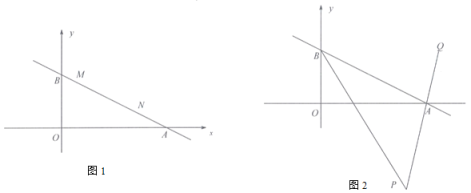
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]()
![]() 轴交反比例函数的图象于点
轴交反比例函数的图象于点![]() ,求点D的坐标和
,求点D的坐标和![]() 的面积;
的面积;
(3)观察图象,写出当x>0时不等式![]() 的解集.
的解集.
【答案】(1)k=8, (3,0);(2) ![]()
![]() ,
,![]() ;(3)
;(3) ![]() .
.
【解析】试题分析:(1)把点A的坐标代入反比例函数解析式中即可求出k值,再令直线y=2x-6中y=0求出x的值,即可得出点B的坐标;
(2)根据BD⊥x轴可知B与D的横坐标相同,将B点的横坐标代入反比例函数解析式即可得出D点的坐标;求出BD的长和点A到BD的距离,根据三角形的面积公式即可得出答案;
(3)根据图象求出双曲线在直线上方时自变量的取值范围即可.
试题解析:
解:(1)![]() 点
点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
![]() ,解得
,解得![]() .
.
将![]() 代入
代入![]() ,得
,得![]() ,解得
,解得![]() .
.
![]() 点
点![]() 的坐标是(3,0).
的坐标是(3,0).
(2)![]() 反比例函数解析式为:
反比例函数解析式为: ![]()
将![]() 代入得
代入得![]() ,
, ![]() 点
点![]() 的坐标是
的坐标是![]() .
.
∴BD=![]() ,点A到BD的距离为4-3=1,
,点A到BD的距离为4-3=1,
![]() 的面积为
的面积为![]()
(3)观察两函数图象可发现:当0<x<4时,反比例函数图象在一次例函数图象的上方,
∴x>0时不等式![]() 的解集为0<x<4.
的解集为0<x<4.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案【题目】(本题10分)某自行车厂一周计划生产700辆自行车,平均每天生产自行车100辆,由于各种原因,实际每天生产量与计划每天生产量相比有出入。下表是某周的自行车生产情况(超计划生产量为正、不足计划生产量为负,单位:辆):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +8 | -2 | -3 | +16 | -9 | +10 | -11 |
(1)根据记录可知前三天共生产自行车 辆;
(2)产量最多的一天比产量最少的一天生产 辆;
(3)若该厂实行按生产的自行车数量的多少计工资,即计件工资制。如果每生产一辆自行车就可以得人民币60 元,超额完多成任务,每超一辆可多得 15 元;若不足计划数的,每少生产一辆扣 15 元,那么该厂工人这一周的工资总额是多少?