题目内容
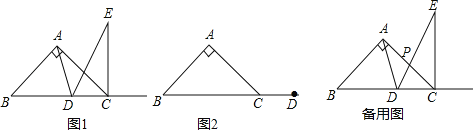
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的弦,过点
的弦,过点![]() 的切线
的切线![]() 交
交![]() 延长线于点
延长线于点![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的度数;
的度数;
(Ⅱ)若![]() ,求
,求![]() 的长.
的长.
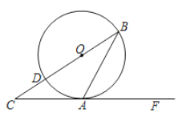
【答案】(Ⅰ)∠BAF=57.5°;(Ⅱ)AB=2![]()
【解析】
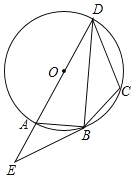
(Ⅰ)连接OA,AD,根据切线的性质得到OA⊥CF,求得∠OAC=90°,根据三角形的内角和得到∠COA=65°,根据等腰三角形的性质得到∠OAB=32.5°,于是得到结论;
(Ⅱ)根据等腰三角形的性质得到∠B=∠C,求得∠C=30°,根据直角三角形的性质得到OA=![]() OC,于是得到结论.
OC,于是得到结论.
解:(Ⅰ)连接OA,AD,
∵CF是⊙O的切线,
∴OA⊥CF,
∴∠OAC=∠OAF=90°,
∵∠C=25°,
∴∠COA=90°-25°=65°,
∵∠COA=∠B+∠OAB,OA=OB,
∴∠B=∠OAB,
∴∠OAB=32.5°,
∴∠BAF=∠OAF∠OAB=90°32.5°=57.5°,
∴∠BAF=57.5°;

(Ⅱ)∵AB=AC,
∴∠B=∠C,
∵∠COA=2∠B,
∴3∠C=90°,
∴∠C=30°,
∴OA=![]() OC,
OC,
∵OA=OD,
∴CD=DO=OA=2,
∴CO=4,AC=![]() 2
2![]() ,
,
∴AB=AC=2![]() .
.

练习册系列答案
相关题目
【题目】某林业部门统计某种树苗在本地区一定条件下的移植成活率,结果如表:
移植的棵数 | 300 | 700 | 1000 | 5000 | 15000 |
成活的棵数 | 280 | 622 | 912 | 4475 | 13545 |
成活的频率 | 0.933 | 0.889 | 0.912 | 0.895 | 0.903 |
根据表中的数据,估计这种树苗移植成活的概率为_____(精确到0.1);如果该地区计划成活4.5万棵幼树,那么需要移植这种幼树大约_____万棵.