题目内容
已知:二次函数的表达式为y=-
x2+x+
.
(1)写出这个函数图象的对称轴和顶点坐标;并画出图象.
(2)求图象与x轴的交点坐标;
(3)观察图象,指出使函数值y>
时自变量x的取值范围.
| 1 |
| 2 |
| 3 |
| 2 |
(1)写出这个函数图象的对称轴和顶点坐标;并画出图象.
(2)求图象与x轴的交点坐标;
(3)观察图象,指出使函数值y>
| 3 |
| 2 |
(1)∵y=-
x2+x+
=-
(x2-2x)+
=-
(x-1)2+2,
∴抛物线的顶点坐标为(1,2),对称轴为直线x=1,
图象如下:
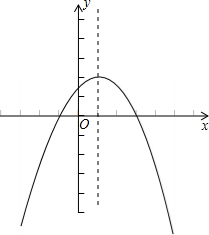
(2)当y=0时,解方程-
x2+x+
=0,
解得x=3或-1,
所以图象与x轴交点为(-1,0),(3,0);
(3)∵抛物线与y轴的交点为(0,
),即x=0时,y=
;
又∵抛物线的对称轴为直线x=1,
∴x=2时,y=
;
由图象可知,函数值y>
时,x的取值范围是0<x<2.
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴抛物线的顶点坐标为(1,2),对称轴为直线x=1,
图象如下:

(2)当y=0时,解方程-
| 1 |
| 2 |
| 3 |
| 2 |
解得x=3或-1,
所以图象与x轴交点为(-1,0),(3,0);
(3)∵抛物线与y轴的交点为(0,
| 3 |
| 2 |
| 3 |
| 2 |
又∵抛物线的对称轴为直线x=1,
∴x=2时,y=
| 3 |
| 2 |
由图象可知,函数值y>
| 3 |
| 2 |

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 次函数的图象.它们的顶点在一条直线上,这条直线的解析式是y=______.
次函数的图象.它们的顶点在一条直线上,这条直线的解析式是y=______.