题目内容
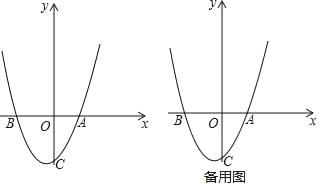
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(3,0),B(﹣5,0),C(0,﹣5)三点,O为坐标原点.
(1)求此抛物线的解析式;
(2)把抛物线y=ax2+bx+c(a≠0)向上平移![]() 个单位长度,再向左平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;
个单位长度,再向左平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;
(3)设点P在y轴上,且满足∠OPA+∠OCA=∠CBA,求CP的长.
【答案】(1)y=![]() x2+
x2+![]() x﹣5;(2)0<n<3;(3)PC=7或17.
x﹣5;(2)0<n<3;(3)PC=7或17.
【解析】
(1)设抛物线解析式为y=a(x﹣3)(x+5),将点C(0,﹣5)的坐标代入抛物线解析式中,利用待定系数法即可求得抛物线的解析式;
(2)先求得平移后新抛物线的顶点坐标,再根据新抛物线的顶点M在△ABC内求得n的取值范围;
(3)分点P在y轴负半轴上和点P在y轴正半轴上两种情况进行讨论,求出两种情况下CP的长度。
(1)∵抛物线y=ax2+bx+c(a≠0)经过A(3,0),B(﹣5,0),
∴设抛物线解析式为y=a(x﹣3)(x+5),
∵抛物线过点C(0,﹣5),∴a×(﹣3)×5=﹣5,
∴a=![]() ,
,
∴抛物线解析式为y=![]() (x﹣3)(x+5)=
(x﹣3)(x+5)=![]() x2+
x2+![]() x﹣5,
x﹣5,
(2)记原抛物线的顶点为M',
由(1)知,抛物线解析式为y=![]() (x﹣3)(x+5)=
(x﹣3)(x+5)=![]() (x2+2x﹣15)=
(x2+2x﹣15)=![]() (x+1)2﹣
(x+1)2﹣![]() ,
,
∴M'(﹣1,﹣![]() ),
),
由平移知,M(﹣1﹣n,﹣1),
∵B(﹣5,0),C(0,﹣5),
∴直线BC的解析式为y=﹣x﹣5,
当y=﹣1时,﹣x﹣5=﹣1,
∴x=﹣4,
∴﹣4<﹣1﹣n<﹣1,
∴0<n<3;
(3)存在,
理由:①当P在y轴正半轴上时,如图,
过点P作PD⊥AC于D,
根据三角形的外角的性质得,∠OPA+∠OCA=∠PAD,
又∵∠OPA+∠OCA=∠CBA=45°,
∴∠PAD=∠CBA=45°,
∴AD=PD,
∵AO=3,CO=5,
∴AC=![]() ,
,
设AD=PD=m,则CD=AC+AD=m+![]() ,
,
又∵∠PDA=∠COA=90°,∠PCD=∠ACO,
∴△COA~△CDP,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]()
∴m=![]() ,
,
∴PC=![]() ×
×![]() =17,
=17,
②当P在y轴负半轴上时,记作P',
由①知,OP=PC﹣CO=17﹣5=12,取OP'=OP=12,如图,
则由对称知:∠OP'A=∠OPA, P'O=PO=12,
∴∠OP'A+∠OCA=∠OPA+∠OCA=∠CBA═45°,
同理P'也满足题目条件,∴P'C=OP'﹣OC=12﹣5=7,
综合以上得:PC=7或17.

 阅读快车系列答案
阅读快车系列答案