题目内容
【题目】如图所示，在四边形ABCD中，AD∥BC，要使四边形ABCD成为平行四边形还需要条件（ ）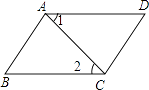 
A.AB=DC
B.∠1=∠2
C.AB=AD
D.∠D=∠B
【答案】D
【解析】解：A、符合条件AD∥BC，AB=DC，可能是等腰梯形，故A选项错误；
B、根据∠1=∠2，推出AD∥BC，不能推出平行四边形，故B选项错误；
C、根据AB=AD和AD∥BC不能推出平行四边形，故C选项错误；
D、∵AD∥BC，
∴∠1=∠2，
∵∠B=∠D，
∴∠BAC=∠DCA，
∴AB∥CD，
∴四边形ABCD是平行四边形，故D选项正确．
故选：D．
【考点精析】根据题目的已知条件，利用平行线的判定与性质和三角形的内角和外角的相关知识可以得到问题的答案，需要掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质；三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角．
练习册系列答案
相关题目
