题目内容
如图,在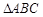 中,点D、E分别在BC、AC上,BE平分
中,点D、E分别在BC、AC上,BE平分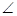 ABC,DE∥BA,若AB=7,BC=8.则线段
ABC,DE∥BA,若AB=7,BC=8.则线段 的长度为 .
的长度为 .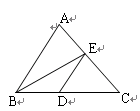
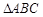 中,点D、E分别在BC、AC上,BE平分
中,点D、E分别在BC、AC上,BE平分 ABC,DE∥BA,若AB=7,BC=8.则线段
ABC,DE∥BA,若AB=7,BC=8.则线段 的长度为 .
的长度为 .
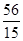
试题分析:由BE平分∠ABC,DE∥BA可知,∠ABE=∠DBE=∠DEB,可得BD=DE(设为x),利用平行线得△ABC∽△EDC,由相似比求DE.
∵BE平分∠ABC,DE∥BA,
∴∠ABE=∠DBE=∠DEB,
∴BD=DE,
设DE=x,
又∵DE∥BA,
∴△ABC∽△EDC,
∴
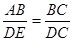 ,
,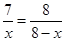 ,解得
,解得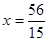
则线段
 的长度为
的长度为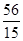 .
.点评:解题的关键是根据已知条件得出相等角,继而可证得等腰三角形,利用平行线构造相似三角形.

练习册系列答案
相关题目
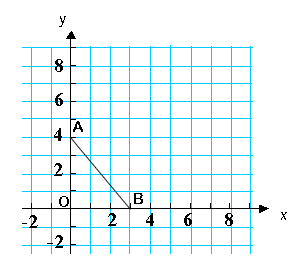
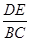 = .
= .

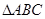 的高CD和BE相交于点O,则图中与
的高CD和BE相交于点O,则图中与 相似的三角形有 ( )
相似的三角形有 ( )
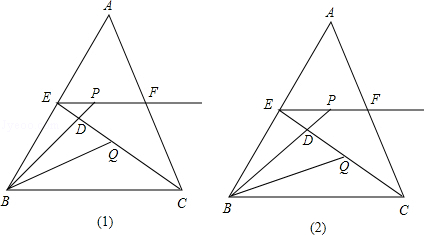
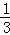 EF时,求S△DPE:S△DBC的值;
EF时,求S△DPE:S△DBC的值;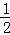 CE时,求y与x之间的函数关系式;
CE时,求y与x之间的函数关系式; CE(n为不小于2的常数)时,直接写出y与x之间的函数关系式.
CE(n为不小于2的常数)时,直接写出y与x之间的函数关系式.