Question

【题目】已知∠AOB=90°，OC是∠AOB的平分线，按以下要求解答问题．

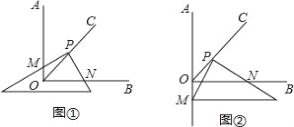
（1）将三角板的直角顶点P在射线OC上移动，两直角边分别与OA，OB交于M，N，如图①，求证：PM=PN；

（2）将三角板的直角顶点P在射线OC上移动，一条直角边与OB交于N，另一条直角边与射线OA的反向延长线交于点M，并猜想此时①中的结论PM=PN是否成立，并说明理由 ．

Answer 1

【答案】(1)见解析(2)成立

【解析】

（1）过P作PE⊥OA，PF⊥OB，由OC为∠AOB的平分线，利用角平分线定理得到PE=PF，利用同角的余角相等得到一对角相等，利用ASA得到△PME与△PNF全等，利用全等三角形的对应边相等即可得证；
（2）过P作PE⊥OA，PF⊥OB，由OC为∠AOB的平分线，利用角平分线定理得到PE=PF，利用同角的余角相等得到一对角相等，利用ASA得到△PME与△PNF全等，利用全等三角形的对应边相等即可得证．

(1)过P作PE⊥OA于E，PF⊥OB于F，

∵OC是∠AOB的平分线，

∴

∵

∴∠MPE=∠NPF，

在△PME和△PNF中，

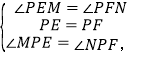
∴△PME≌△PNF(ASA)，

∴PM=PN.

(2)过P作PE⊥OA于E，PF⊥OB于F，

∵OC是∠AOB的平分线，

∴

∵

∴∠MPE=∠NPF，

在△PME和△PNF中，

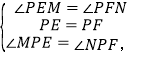
∴△PME≌△PNF(ASA)，

∴PM=PN.