题目内容
【题目】在由6个边长为1的小正方形组成的方格中:
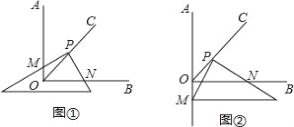
(1)如图(1),A、B、C是三个格点(即小正方形的顶点),判断AB与BC的关系,并说明理由;
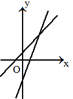
(2)如图(2),连结三格和两格的对角线,求∠α+∠β的度数(要求:画出示意图并给出证明)

【答案】(1) AB与BC是垂直且相等.(2) 45°.
【解析】
试题(1)如图(1),根据勾股定理,判断出AB2+BC2=AC2,即可推得△ABC是直角三角形,据此判断出AB与BC的关系,并说明理由即可.
(2)如图(2),根据勾股定理,判断出AB2+BC2=AC2,即可推得△ABC是等腰直角三角形,据此求出∠α+∠β的度数是多少即可.
试题解析:
(1)如图(1),连接AC,
 ,
,
由勾股定理得,AB2=12+22=5,
BC2=12+22=5,
AC2=12+32=10,
∴AB2+BC2=AC2,AB=BC,
∴△ABC是直角三角形,∠ABC=90°,
∴AB⊥BC
∴AB与BC是垂直且相等.
(2)∠α+∠β=45°.
证明:如图(2),
 ,
,
由勾股定理得,AB2=12+22=5,
BC2=12+22=5,
AC2=12+32=10,
∴AB2+BC2=AC2,
∴△ABC是直角三角形,
∵AB=BC,
∴△ABC是等腰直角三角形,
∴∠α+∠β=45°.

 阅读快车系列答案
阅读快车系列答案【题目】某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.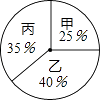
(1)分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,三人中谁的得分最高?