题目内容
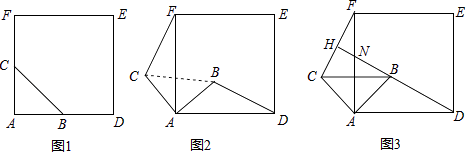
【题目】如图，在矩形ABCD中，AB=10，AD=6，点M为AB上的一动点，将矩形ABCD沿某一直线对折，使点C与点M重合，该直线与AB（或BC）、CD（或DA）分别交于点P、Q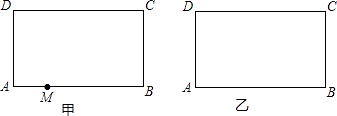
（1）用直尺和圆规在图甲中画出折痕所在直线（不要求写画法，但要求保留作图痕迹）
（2）如果PQ与AB、CD都相交，试判断△MPQ的形状并证明你的结论；
（3）设AM=x，d为点M到直线PQ的距离，y=d2 ，
①求y关于x的函数解析式，并指出x的取值范围；
②当直线PQ恰好通过点D时，求点M到直线PQ的距离．
【答案】
（1）
解：如图1所示：
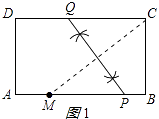
（2）
解：△MPQ是等腰三角形；理由如下：
∵四边形ABCD是矩形，
∴AB∥CD，CD=AB=10，
∴∠QCO=∠PMO，
由折叠的性质得：PQ是CM的垂直平分线，
∴CQ=MQ，OC=OM，
在△OCQ和△OMP中，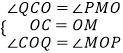 
，
∴△OCQ≌△OMP（ASA），
∴CQ=MP，
∴MP=MQ，
即△MPQ是等腰三角形
（3）
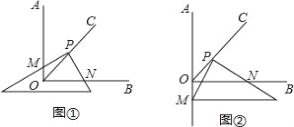
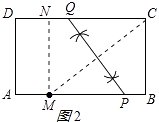
解：①作MN⊥CD于N，如图2所示：
则MN=AD=6，DN=AM=x，CN=10﹣x，
在Rt△MCN中，由勾股定理得：CM2=MN2+CN2，
即（2d）2=62+（10﹣x）2，
整理得：d2= 
x2﹣5x+34，
即y= x2﹣5x+34（0≤x≤10）；
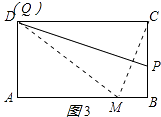
②当直线PQ恰好通过点D时，如图3所示：
则Q与D重合，DM=DC=10，
在Rt△ADM中，AM= 
=8，
∴BM=10﹣8=2，
∴CM= 
= 
=2 
，
∴d= 
CM= ，
即点M到直线PQ的距离为 ．
【解析】（1）作线段CM的垂直平分线即可；（2）由矩形的性质得出AB∥CD，CD=AB=10，得出∠QCO=∠PMO，由折叠的性质得出PQ是CM的垂直平分线，由线段垂直平分线的性质得出CQ=MQ，由ASA证明△OCQ≌△OMP，得出CQ=MP，得出MP=MQ即可；（3）①作MN⊥CD于N，如图2所示：则MN=AD=6，DN=AM=x，CN=10﹣x，在Rt△MCN中，由勾股定理得出（2d）2=62+（10﹣x）2 ， 即可得出结果；②当直线PQ恰好通过点D时，Q与D重合，DM=DC=10，由勾股定理求出AM，得出BM，再由勾股定理求出CM，即可得出结果．本题是四边形综合题目，考查了矩形的性质、折叠的性质、线段垂直平分线的性质、全等三角形的判定与性质、等腰三角形的判定、勾股定理等知识；本题综合性强，有一定难度，证明三角形全等和运用勾股定理是解决问题的关键．
