题目内容
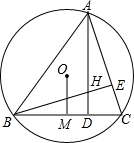
如图,已知△ABC的周长为2p,在AB、AC上分别取点M和N,使MN∥BC,且MN与△ABC的内切圆相切.
求:MN的最值.
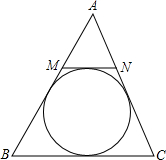
求:MN的最值.

设BC=a,BC边上的高为h,
内切圆半径为r.
∵△AMN∽△ABC,
=
,
MN=a(1-
),
由S△ABC=
ar+
br+
cr=
(a+b+c)r=
•2pr=rp,
∴r=
=
,
∴MN=a(1-
)=p•
(1-
)≤p[
]2=
,
当且仅当
=1-
,
即a=
时,取等号,
∴MN的最大值为
.
内切圆半径为r.
∵△AMN∽△ABC,
| MN |
| BC |
| h-2r |
| h |
MN=a(1-
| 2r |
| h |
由S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴r=
| S△ABC |
| p |
| ah |
| 2p |
∴MN=a(1-
| a |
| p |
| a |
| p |
| a |
| p |
| ||||
| 2 |
| p |
| 4 |
当且仅当
| a |
| p |
| a |
| p |
即a=
| p |
| 2 |
∴MN的最大值为
| p |
| 4 |

练习册系列答案
相关题目