题目内容
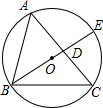
△ABC中,AB=AC,∠A为锐角,CD为AB边上的高,I为△ACD的内切圆圆心,则∠AIB的度数是______.
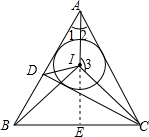
如图,连IC;
∵I为△ACD的内切圆圆心,
∴AI是角平分线;
又∵AB=AC,
∴AI垂直平分BC,E为垂足,
∴∠1=∠2,
∴∠AIB=∠3;
又∵CD⊥AB,I是内心,
∴∠3=90°+
×90°=135°,
∴∠AIB=135°.
故填135°.
∵I为△ACD的内切圆圆心,
∴AI是角平分线;
又∵AB=AC,
∴AI垂直平分BC,E为垂足,
∴∠1=∠2,
∴∠AIB=∠3;
又∵CD⊥AB,I是内心,
∴∠3=90°+
| 1 |
| 2 |
∴∠AIB=135°.
故填135°.


练习册系列答案
相关题目