题目内容
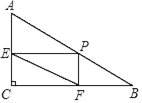
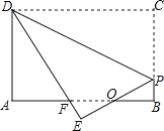
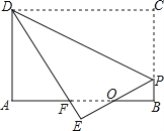
【题目】如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE.、DE分别交AB于点O、F,且OP=OF,则BP的长为______.
【答案】![]()
【解析】
根据折叠的性质可得出DC=DE、CP=EP,由∠EOF=∠BOP、∠B=∠E、OP=OF可得出△OEF≌△OBP,根据全等三角形的性质可得出OE=OB、EF=BP,设BF=EP=CP=x,则AF=4-x,BP=3-x=EF,DF=DE-EF=4-(3-x)=x+1,依据Rt△ADF中,AF2+AD2=DF2,求出x的值,即可得出BP的长.
解:根据折叠可知:△DCP≌△DEP,
∴DC=DE=4,CP=EP.
在△OEF和△OBP中,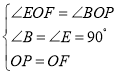 ,
,
∴△OEF≌△OBP(AAS),
∴OE=OB,EF=BP,
∴BF=EP=CP,
设BF=EP=CP=x,则AF=4-x,BP=3-x=EF,DF=DE-EF=4-(3-x)=x+1,
∵∠A=90°,
∴Rt△ADF中,AF2+AD2=DF2,
即(4-x)2+32=(1+x)2,
解得:x=![]() ,
,
∴BP=3-x=3-![]() =
=![]() ,
,
故答案为:![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的初三(1)班、(2)班进行了检测,如图表示从两班各随机抽取的10名学生的得分情况.
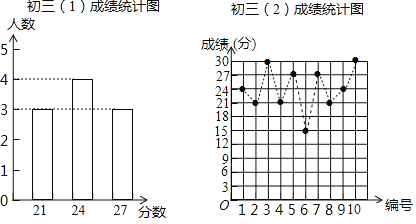
(1)利用图中提供的信息,补全下表:
班级 | 平均数/分 | 中位数/分 | 众数/分 |
初三(1)班 | __________ | 24 | ________ |
初三(2)班 | 24 | _________ | 21 |
(2)若把24分以上(含24分)记为“优秀”,两班各40名学生,请估计两班各有多少名学生成绩优秀;
(3)观察上图的数据分布情况,请通过计算说明哪个班的学生纠错的得分更稳定.