Question

【题目】已知为等边三角形，在的延长线上，为线段上的一点，．

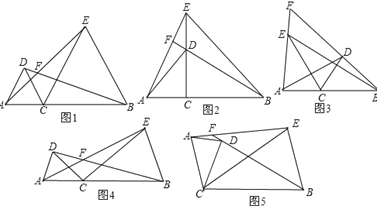
（1）如图，求证：；

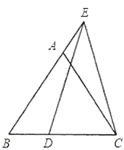
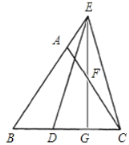
（2）如图，过点作于点，交于点，当时，在不添加任何辅助线的情况下，直接写出图中所有的等腰三角形．

Answer 1

【答案】（1）见解析；（2），，，．

【解析】

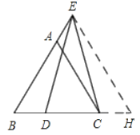
（1）延长至点，使，连接，利用(SAS)证得，得到，证得也是等边三角形，利用等量代换即可证得结论；

（2）根据等腰三角形的概念即可解答．

（1）延长至点，使，连接，

∵，

∴，

∵，，

∴，

∴(SAS) ，

∴，

∵是等边三角形，

∴，

∴是等边三角形，

∴，

∵，

∴，

∴，

（2）由已知：为等边三角形，以及，

∴，是等腰三角形；

∵为等边三角形，

∴，

∵，

∴，

，

∴，

∴是等腰三角形，

∵，，，，

∴，

，

∴，

∴是等腰三角形，

综上，，，，是等腰三角形．