题目内容
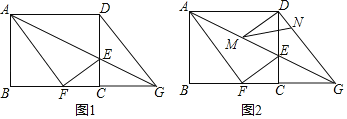
【题目】如图1,在矩形ABCD中,AB=8,AD=10,E是CD边上一点,连接AE,将矩形ABCD沿AE折叠,顶点D恰好落在BC边上点F处,延长AE交BC的延长线于点G.
(1)求线段CE的长;
(2)如图2,M,N分别是线段AG,DG上的动点(与端点不重合),且∠DMN=∠DAM,设AM=x,DN=y.
①写出y关于x的函数解析式,并求出y的最小值;
②是否存在这样的点M,使△DMN是等腰三角形?若存在,请求出x的值;若不存在,请说明理由.
【答案】(1)3;(2)①y=![]() x2﹣
x2﹣![]() x+10,y有最小值为2;②存在,8
x+10,y有最小值为2;②存在,8![]() ﹣10或
﹣10或![]() .
.
【解析】
(1)由翻折可知:AD=AF=10,DE=EF,求出BF,设EC=x,则DE=EF=8﹣x,在Rt△ECF中,利用勾股定理构建方程即可解决问题;
(2)①首先求出AG,DG,∠ADM=∠NMG,证明△ADM∽△GMN,可得![]() ,整理后根据二次函数的最值求解即可.
,整理后根据二次函数的最值求解即可.
②存在.有两种情形:如图3﹣1中,当MN=MD时.如图3﹣2中,当MN=DN时,分别通过证明三角形相似,利用相似三角形的性质求解即可.
解:(1)如图1中,
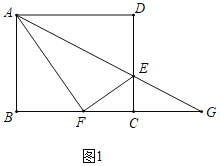
∵四边形ABCD是矩形,
∴AD=BC=10,AB=CD=8,∠B=∠BCD=90°,
由翻折可知:AD=AF=10,DE=EF,
在Rt△ABF中,BF=![]() =6,
=6,
∴CF=BC﹣BF=10﹣6=4,
设CE=x,则DE=EF=8﹣x,
在Rt△EFC中,则有:(8﹣x)2=x2+42,
∴x=3,即CE=3.
(2)①如图2中,
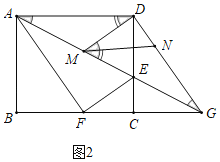 ,
,
∵AD∥CG,
∴![]() ,
,
∴![]() ,
,
∴CG=6,
∴BG=BC+CG=16,
在Rt△ABG中,AG=![]() ,
,
在Rt△DCG中,DG=![]() ,
,
∵AD=DG=10,
∴∠DAG=∠AGD,
∵∠DMG=∠DMN+∠NMG=∠DAM+∠ADM,∠DMN=∠DAM,
∴∠ADM=∠NMG,
∴△ADM∽△GMN,
∴![]() ,
,
∴![]() ,
,
∴y=![]() x2﹣
x2﹣![]() x+10,
x+10,
∴当x=4![]() 时,y有最小值,将x=4
时,y有最小值,将x=4![]() 代入可得,最小值=2;
代入可得,最小值=2;
②存在,
由①可得∠DMN=∠DGM,
∴∠DNM=∠DMG,
∴∠DNM≠∠DMN,
所以有两种情形:如图3﹣1中,当MN=MD时,
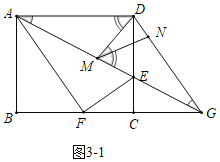
∵∠MDN=∠GDM,∠DMN=∠DGM,
∴△DMN∽△DGM,
∴![]() ,
,
∵MN=DM,
∴DG=GM=10,
∴x=AM=8![]() ﹣10.
﹣10.
如图3﹣2中,当MN=DN时,作MH⊥DG于H.
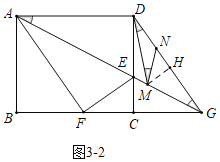
∵MN=DN,
∴∠MDN=∠DMN,
∵∠DMN=∠DGM,
∴∠MDG=∠MGD,
∴MD=MG,
∵MH⊥DG,
∴DH=GH=5,
∵∠DAG=∠DGA,∠DAG=∠AGB,
∴∠DGA=∠AGB,
又∵∠MHG=∠ABG=90°,
∴△GHM∽△GBA,
∴![]() ,
,
∴![]() ,
,
∴MG=![]() ,
,
∴x=AM=8![]() ﹣
﹣![]() =
=![]() .
.
综上所述,满足条件的x的值为8![]() ﹣10或
﹣10或![]() .
.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案