题目内容
【题目】如图，在△ABC中，∠ACB＝90°，BC＝2，∠A＝30°，将△ABC绕点C顺时针旋转120°，若P为AB上一动点，旋转后点P的对应点为点P'，则线段PP'长度的最小值是（ ）
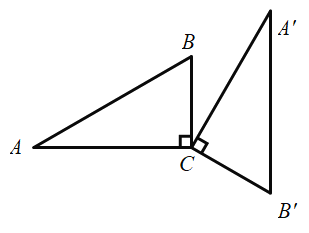
A.
B.2C.3D.2
【答案】C
【解析】
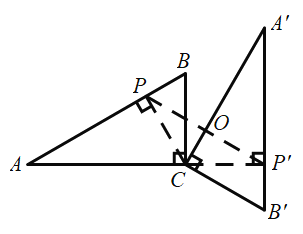
如图，过C点作CP⊥AB于P点，CP'⊥A'B'于P'点，CO⊥PP'于O点，此时线段PP'为最小值，根据旋转的性质与特殊角的三角函数可得PP'
，然后在Rt△BCP中求得CP的长即可.
如图，过C点作CP⊥AB于P点，CP'⊥A'B'于P'点，CO⊥PP'于O点，此时线段PP'为最小值，
由题意可设CP=CP'，
∵∠PCP'=120°，
∴∠CPP'=∠CP'P=30°，
∴PO=CPcos30°=
，即PP'，
当CP⊥AB时，CP为最小值，则此时PP'为最小值，
在Rt△BCP中，∠B=60°，BC=2，
∴CP=BCsin60°
，
∴PP'
.
故选C.
练习册系列答案
相关题目
