题目内容
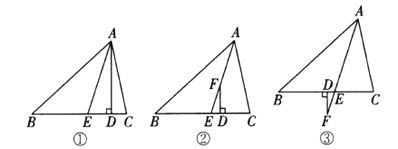
【题目】如图,B、D、C三点在一条直线上,∠ADB=∠ADC=90°,BD=DE,∠DAC=45°;
(1)线段AB、CE的关系为 ;
(2)若BD=a,AD=b,AB=c,请利用此图的面积式证明勾股定理.

【答案】(1)AB=CE,AB⊥CE;(2)证明见解析.
【解析】试题分析:(1)先由边角边证得△ADB≌△CDE,可得AB=CE,∠BAD=∠ECD;延长CE和AB交于点F,由同角的余角相等即可证得∠BFC=90°,即AB⊥CE;
(2)把△ABC面积分成![]() ,由三角形的面积公式即可证明.
,由三角形的面积公式即可证明.
试题解析:(1)线段AB、CE的关系为:AB=CE,AB⊥CE,
∵∠ADB=∠ADC=90°,∠DAC=45°,
∴△ACD是等腰直角三角形,
∴AD=CD,
∵BD=ED,
∴△ADB≌△CDE(SAS),
∴∠BAD=∠ECD,
延长CE交AB于点F,如图:

∵∠BAD+∠ABD=90°,
∴∠ECD +∠ABD=90°,
即AB⊥CE;
(2)如图,设EF=x,

∵![]() ,
,
∴![]() ,
,
∵BD=a,AB=c,AD=b,
∴易得 AB=CE=c,BD=DE=a,AD=CD=b,
∴![]() ,
,
即: ![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目