题目内容
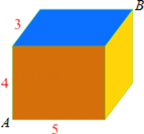
【题目】如图所示，有一个长方体，它的长、宽、高分别为5cm，3cm，4cm．在顶点A处有一只蚂蚁，它想吃到与顶点A相对的顶点B的食物．
（1）请画出该蚂蚁沿长方体表面爬行的三条线路图（即平面展开图）；
（2）已知蚂蚁沿长方体表面爬行的速度是0.8cm/s，问蚂蚁能否在11秒内获取到食物？
【答案】（1）见解析；（2）蚂蚁能在11秒内获取到食物．
【解析】
（1）分类讨论画出解答几何体的部分侧面展开图，即可得到蚂蚁沿长方体表面爬行的三条线路图；
（2）利用直角三角形的边的关系容易解得AB的值，从而得出其中的最小值，再利用速度、时间、路程之间的关系，求出时间和11秒比较大小即可．
解：（1）如图所示：
从长方体的一条对角线的一个端点A出发，沿表面运动到另一个端点B，有三种方案，如图是它们的三种部分侧面展开图；
（2）由（1）可知AB路程可能是：
AB=
=
或
=
或
=
，
∴它想吃到与顶点A相对的顶点B的食物最短路程为，
∴所需时间为÷0.8≈10.75＜11，
∴蚂蚁能在11秒内获取到食物．
阅读快车系列答案
【题目】温州某企业安排65名工人生产甲、乙两种产品，每人每天生产2件甲或1件乙，甲产品每件可获利15元．根据市场需求和生产经验，乙产品每天产量不少于5件，当每天生产5件时，每件可获利120元，每增加1件，当天平均每件获利减少2元．设每天安排x人生产乙产品．
（1）根据信息填表
产品种类 | 每天工人数（人） | 每天产量（件） | 每件产品可获利润（元） |
甲 | 15 | ||
乙 |
|
|
（2）若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元，求每件乙产品可获得的利润．
（3）该企业在不增加工人的情况下，增加生产丙产品，要求每天甲、丙两种产品的产量相等．已知每人每天可生产1件丙（每人每天只能生产一件产品），丙产品每件可获利30元，求每天生产三种产品可获得的总利润W（元）的最大值及相应的x值．
