��Ŀ����
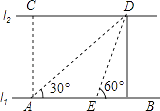
����Ŀ����1����ͼ1�����ı���ABCD�У�AB��AD����BAD��120������B����ADC��90����EF�ֱ��� BC��CD�ϵĵ㣬����EAF��60����̽��ͼ���߶�BE��EF��FD֮���������ϵ��
С��ͬѧ̽��������ķ������ӳ�FD����G��ʹDG��BE������AG����֤����ABE�ա�ADG����֤����AEF�ա�AGF���ɵó����ۣ����Ľ���Ӧ�� ��
̽�����죺
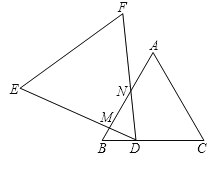
��2����ͼ2�������ı���ABCD�У�AB��AD����B����D��180����E��F�ֱ���BC��CD�ϵĵ㣬����EAF��![]() ��BAD�����������Ƿ���Ȼ��������˵�����ɣ�
��BAD�����������Ƿ���Ȼ��������˵�����ɣ�

���𰸡����ⱳ����BE +DF =EF��̽�����죺������Ȼ���������ɼ�����.
��������
���ⱳ����֤����ABE�ա�ADG���ɵ�AE=AG����֤����AEF�ա�AGF���ɵ�EF=FG�����ɽ��⣻
̽�����죺�ӳ�FD��G��ʹDG=BE������AG������ͬ�ǵIJ�����������B=��ADG��Ȼ���������߽DZ���֤����ABE����ADGȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�AE=AG����BAE=��DAG���������EAF=��GAF��Ȼ���������߽DZ���֤����AEF����GAFȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�EF=GF��Ȼ����⼴�ɣ�
���ⱳ��������ABE����ADG�У�
 ��
��
���ABE�ա�ADG��SAS����
��AE=AG����BAE=��DAG��
�ߡ�EAF=![]() ��BAD��
��BAD��
���GAF=��DAG+��DAF=��BAE+��DAF=��BAD-��EAF=��EAF��
���EAF=��GAF��
����AEF����GAF��
 ��
��
���AEF�ա�AGF��SAS����
��EF=FG��
��FG=DG+DF=BE+DF��
��EF=BE+DF��
�ʴ�Ϊ��EF=BE+DF��
̽�����죺 ������Ȼ�������������£�
��ͼ�ڣ��ӳ�FD��G��ʹDG =BE������AG��

�ߡ�B +��ADC =180�㣬��ADC +��ADG =180�㣬
���B =��ADG��
����ABE����ADG��
 ��
��
���ABE�ա�ADG��SAS����
��AE=AG����BAE=��DAG��
�ߡ�EAF=![]() ��BAD��
��BAD��
���GAF=��DAG+��DAF=��BAE+��DAF=��BAD-��EAF=��EAF��
���EAF=��GAF��
����AEF����GAF��
 ��
��
���AEF�ա�AGF��SAS����
��EF=FG��
��FG=DG+DF=BE+DF��
��EF=BE+DF.

����Ŀ��ij�����ƻ�����A��B���ֲ�Ʒ��10�����������ɱ����������±���
A�ֲ�Ʒ | B�ֲ�Ʒ | |
�ɱ�����Ԫ/���� | 2 | 5 |
������Ԫ/���� | 1 | 3 |
��1���������ƻ�����14��Ԫ����A��B���ֲ�ƷӦ�ֱ��������ټ���
��2���������ƻ�Ͷ���ʽ���44��Ԫ���һ�������14��Ԫ�������������