题目内容
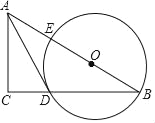
【题目】已知:在![]() 中,以
中,以![]() 边为直径的
边为直径的![]() 交
交![]() 于点
于点![]() ,在劣弧
,在劣弧![]() 上取一点
上取一点![]() 使
使![]() ,延长
,延长![]() 依次交
依次交![]() 于点
于点![]() ,交
,交![]() 于
于![]() .
.
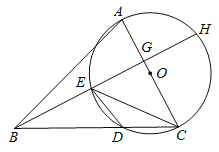
(1)求证:![]() ;
;
(2)若![]() ,
,![]() 的直径等于10,
的直径等于10,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析,(2)![]()
【解析】
(1)连接AD,由圆周角定理即可得出∠DAC=∠DEC,∠ADC=90°,再根据直角三角形的性质即可得出结论;
(2)由∠BDA=180°-∠ADC=90°,∠ABC=45°可求出∠BAD=45°,利用勾股定理即可得出DC的长,进而求出BC的长,由已知的一对角相等和公共角,根据两对对应角相等的两三角形相似可得三角形BCE与三角形EDC相似,由相似得比例即可求出CE的长.
证明:(1)连接AD,

∵∠DAC=∠DEC,∠EBC=∠DEC,
∴∠DAC=∠EBC,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠DCA+∠DAC=90°,
∴∠EBC+∠DCA=90°,
∴∠BGC=180°-(∠EBC+∠DCA)=180°-90°=90°,
∴AC⊥BH;
(2)∵∠BDA=180°-∠ADC=90°,∠ABC=45°,
∴∠BAD=45°,
∴BD=AD,
∵BD=8,
∴AD=8,
在直角三角形ADC中,AD=8,AC=10,
根据勾股定理得:DC=6,
则BC=BD+DC=14,
∵∠EBC=∠DEC,∠BCE=∠ECD,
∴△BCE∽△ECD,
∴ ![]() ,
,
即![]()
∴CE![]()

练习册系列答案
相关题目