题目内容
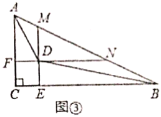
【题目】如图,已知点![]() 、
、![]() ,
,![]() 为
为![]() 轴正半轴上的一个动点,以
轴正半轴上的一个动点,以![]() 为边构造
为边构造![]() ,使点
,使点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() .若
.若![]() 为
为![]() 的中点,则
的中点,则![]() 的最小值为___________.
的最小值为___________.
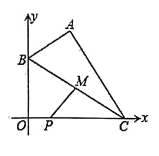
【答案】![]()
【解析】
先确定M点的轨迹为直线,当PM⊥M1M2时,PM最小,可以证明△PMM2∽△M1OM2,即可求解.
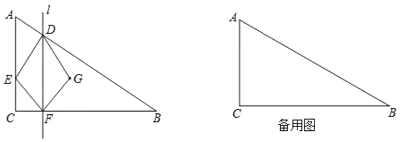
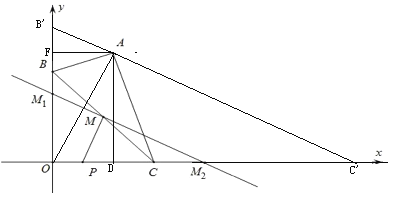
当B在原点时,作OA⊥AC交x轴于C’,作AD⊥x轴于D点
∴AD=4, OD=2
∵∠AOD+∠OAD=∠AOD+∠AC’D=90°
∴∠OAD=∠AC’D
∴tan∠OAD=tan∠AC’D
∴![]()
∴C’D=8
∴BC’=10,故点M2(5,0);
当C在原点时,作AF⊥y轴于F点
同理可得tan∠OAD=tan∠B’AF=![]()
∴BF’=![]() AF=1
AF=1
∴B’(0,5),故M1(0,![]() ),
),
∵当PM⊥M1M2时,PM最小,
∵∠MM2P=∠OM2M1,∠PMM2=∠M1OM2=90°
∴△PMM2∽△M1OM2,
∴![]() ,
,
∵M1M2=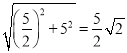 ,M1O=
,M1O=![]() , PM2=5-1=4
, PM2=5-1=4
∴PM=![]() ;
;
故答案为![]() .
.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为![]() 分)、
分)、![]() 分)、
分)、![]() 分)、
分)、![]() 分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
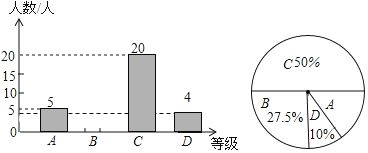
其中组![]() 的期末数学成绩如下
的期末数学成绩如下
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请补全条形统计图;
(2)这部分学生的期末数学成绩的中位数是 ,![]() 组的期末数学成绩的众数是 ;
组的期末数学成绩的众数是 ;
(3)这个学校九年级共有学生![]() 人,若分数为
人,若分数为![]() 分(含
分(含![]() 分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?