ЬтФПФкШн
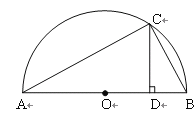
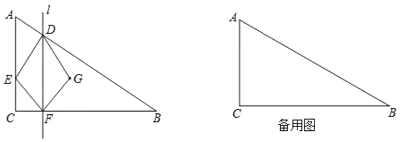
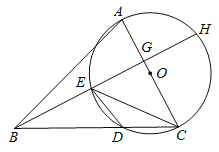
ЁОЬтФПЁПдкЁїABCжаЃЌCAЃНCBЃЌ0ЁуЃМЁЯCЁм90ЁуЃЎЙ§ЕуAзїЩфЯпAPЁЮBCЃЌЕуMЁЂNЗжБ№дкБпBCЁЂACЩЯЃЈЕуMЁЂNВЛгыЫљдкЯпЖЮЖЫЕужиКЯЃЉЃЌЧвBMЃНANЃЌСЌНсBNВЂбгГЄНЛAPгкЕуDЃЌСЌНсMAВЂбгГЄНЛADЕФДЙжБЦНЗжЯпгкЕуEЃЌСЌНсEDЃЎ
ЃЈВТЯыЃЉШчЭМЂйЃЌЕБЁЯCЃН45ЁуЪБЃЌПЩжЄЁїBCNЁеЁїACMЃЌДгЖјЕУГіЁЯCBNЃНЁЯCAMЃЌНјЖјЕУГіЁЯBDEЕФДѓаЁЮЊЁЁ ЁЁЖШЃЎ
ЃЈЬНОПЃЉШчЭМЂкЃЌШєЁЯCЃНІСЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїBCNЁеЁїACMЃЎ
ЃЈ2ЃЉЁЯBDEЕФДѓаЁЮЊЁЁ ЁЁЖШЃЈгУКЌaЕФДњЪ§ЪНБэЪОЃЉЃЎ
ЃЈгІгУЃЉШчЭМЂлЃЌЕБЁЯCЃН90ЁуЪБЃЌСЌНсBEЃЎШєBCЃН3ЃЌЁЯBAMЃН15ЁуЃЌдђЁїBDEЕФУцЛ§ЮЊЁЁ ЁЁЃЎ
ЁОД№АИЁПЁОВТЯыЁП135ЁуЃЛЁОЬНОПЁПЃЈ1ЃЉЯъМћНтЮіЃЛЃЈ2ЃЉІСЛђЃЈ180ЉІСЃЉЃЛЁОгІгУЁП9![]() Љ9ЃЎ
Љ9ЃЎ
ЁОНтЮіЁП
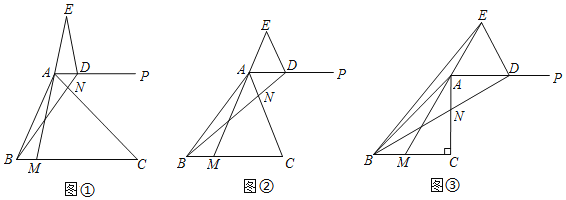
ВТЯыЃКШчЭМЃЈ1ЃЉжаЃЌбгГЄEDНЛBCгкЕуFЃЌНЛACгкЕуOЃЎЯыАьЗЈжЄУїЁЯBNCЃНЁЯBFEЃЌдйРћгУШ§НЧаЮЕФЭтНЧЕФаджЪМДПЩНтОіЮЪЬтЃЛ
ЬНОПЃКЃЈ1ЃЉЭЌРэИљОнSASжЄУїЃКЁїBCNЁеЁїACMЃЛ
ЃЈ2ЃЉЗжСНжжЧщаЮЬжТлЧѓНтМДПЩЃЌЂйШчЭМ2жаЃЌЕБЕуEдкAMЕФбгГЄЯпЩЯЪБЃЌЂкШчЭМ4жаЃЌЕБЕуEдкMAЕФбгГЄЯпЩЯЪБЃЌЗжБ№МЦЫуМДПЩЃЛ
гІгУЃКШчЭМ3ЃЌЗжБ№МЦЫуBDКЭDEЕФГЄЃЌжЄУїЁїEADЪЧЕШБпШ§НЧаЮЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНПЩЕУНсТлЃЎ
ВТЯыЃКжЄУїЃКШчЭМ1жаЃЌбгГЄEDНЛBCгкЕуFЃЌНЛACгкЕуOЃЌ
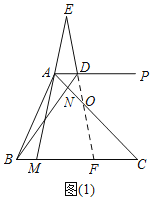
ЁпCBЃНCAЃЌ
ЁрЁЯABMЃНЁЯBANЃЌ
ЁпCAЃНCBЃЌBMЃНANЃЌ
ЁрCMЃНCNЃЌ
ЁпЁЯCЃНЁЯCЃЌ
ЁрЁїBCNЁеЁїACMЃЈSASЃЉЃЌ
ЁрЁЯCBNЃНЁЯCAMЃЌ
ЁпEЪЧADЕФДЙжБЦНЗжЯпЩЯЕФЕуЃЌ
ЁрEAЃНEDЃЌ
ЁрЁЯEADЃНЁЯEDAЃЌ
ЁпADЁЮBCЃЌ
ЁрЁЯEADЃНЁЯEMFЃЌЁЯEDAЃНЁЯEFMЃЌ
ЁрЁЯBNCЃНЁЯBFEЃЌ
ЁрЁЯNOD+ЁЯBDFЃНЁЯC+ЁЯFOCЃЌ
ЁпЁЯCЃН45ЁуЃЌЁЯFOCЃНЁЯNODЃЌ
ЁрЁЯNDOЃН45ЁуЃЌ
ЁрЁЯBDEЃН135ЁуЃЌ
ЙЪД№АИЮЊЃК135ЁуЃЛ
ЬНОПЃК
ЃЈ1ЃЉжЄУїЃКЁпCAЃНCBЃЌBMЃНANЃЌ
ЁрCAЉANЃНCBЉBMЃЌ
ЁрMCЃНNCЃЌ
гжЁпЁЯCЃНЁЯCЃЌ
ЁрЁїBCNЁеЁїACMЃЈSASЃЉЃЛ
ЃЈ2ЃЉЗжСНжжЧщПіЃК
ЂйШчЭМ2жаЃЌЕБЕуEдкAMЕФбгГЄЯпЩЯЪБЃЌ
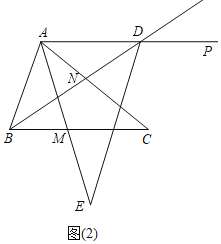
взжЄЃКЁЯCBNЃНЁЯADBЃНЁЯCANЃЌЁЯACBЃНЁЯCADЃЌ
ЁпEAЃНEDЃЌ
ЁрЁЯEADЃНЁЯEDAЃЌ
ЁрЁЯCAM+ЁЯCADЃНЁЯBDE+ЁЯADBЃЌ
ЁрЁЯBDEЃНЁЯCADЃНЁЯACBЃНІСЃЎ
ШчЭМ4жаЃЌЕБЕуEдкMAЕФбгГЄЯпЩЯЪБЃЌбгГЄEDНЛBCЕФбгГЄЯпгкЕуFЃЌ
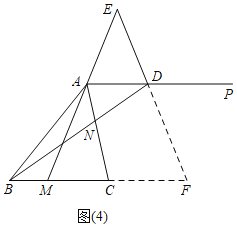
ЭЌРэЕУЁїBCNЁеЁїACMЃЈSASЃЉЃЌ
ЁрЁЯCBNЃНЁЯCAMЃЌ
ЭЌРэЕУЃКЁЯBNCЃНЁЯAMCЃНЁЯBFEЃЌ
ЁрЁЯBNC+ЁЯNBCЃНЁЯNBC+ЁЯBFEЃЌ
ЁрЁЯACBЃНЁЯBDFЃНІСЃЌ
ЁрЁЯBDEЃН180ЁуЉІСЃЎ
ЙЪД№АИЮЊЃКІСЛђЃЈ180ЉІСЃЉЃЛ
гІгУЃК
ШчЭМ3ЃЌЭЌЃЈ2ЃЉЕУЃКЁЯBDEЃН180ЁуЉЁЯACBЃН90ЁуЃЌ
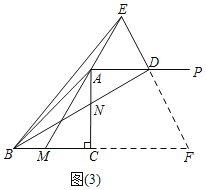
ЁпЁЯACBЃН90ЁуЃЌACЃНBCЃН3ЃЌ
ЁрЁЯBACЃНЁЯABCЃН45ЁуЃЌ
ЁпЁЯBAMЃН15ЁуЃЌ
ЁрЁЯCAMЃНЁЯCBNЃН30ЁуЃЌ
RtЁїBNCжаЃЌCNЃН![]() ЃЌBNЃН
ЃЌBNЃН![]() ЃЌ
ЃЌ
ЁрANЃНACЉCNЃН3Љ![]() ЃЌ
ЃЌ
ЁпADЁЮBCЃЌ
ЁрЁЯDANЃНЁЯACBЃН90ЁуЃЌЁЯADNЃНЁЯNBCЃН30ЁуЃЌ
ЁрDNЃН2ANЃН6Љ2![]() ЃЌADЃН
ЃЌADЃН![]() ANЃН3
ANЃН3![]() Љ3ЃЌ
Љ3ЃЌ
ЁрBDЃНBN+DNЃН2![]() +6Љ2
+6Љ2![]() ЃН6ЃЌ
ЃН6ЃЌ
ЁпEAЃНEDЃЌЁЯEADЃН60ЁуЃЌ
ЁрЁїEADЪЧЕШБпШ§НЧаЮЃЌ
ЁрEDЃНADЃН3![]() Љ3ЃЌ
Љ3ЃЌ
ЁрSЁїBDEЃН![]()
ЙЪД№АИЮЊЃК9![]() Љ9ЃЎ
Љ9ЃЎ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
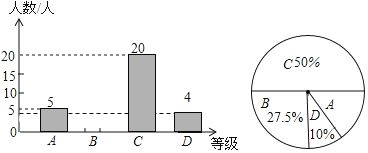
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИЁОЬтФПЁПЮЊСЫНтБОаЃОХФъМЖбЇЩњЦкФЉЪ§бЇПМЪдЧщПіЃЌаЁССдкОХФъМЖЫцЛњГщШЁСЫвЛВПЗжбЇЩњЕФЦкФЉЪ§бЇГЩМЈЮЊбљБОЃЌЗжЮЊ![]() Зж)ЁЂ
Зж)ЁЂ![]() Зж)ЁЂ
Зж)ЁЂ![]() Зж)ЁЂ
Зж)ЁЂ![]() Зж)ЫФИіЕШМЖНјааЭГМЦЃЌВЂНЋЭГМЦНсЙћЛцжЦГЩШчЯТЭГМЦЭМБэЃЌЧыФуИљОнЭГМЦЭМНтД№вдЯТЮЪЬтЃК
Зж)ЫФИіЕШМЖНјааЭГМЦЃЌВЂНЋЭГМЦНсЙћЛцжЦГЩШчЯТЭГМЦЭМБэЃЌЧыФуИљОнЭГМЦЭМНтД№вдЯТЮЪЬтЃК
Цфжазщ![]() ЕФЦкФЉЪ§бЇГЩМЈШчЯТ
ЕФЦкФЉЪ§бЇГЩМЈШчЯТ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЃЈ1ЃЉЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉетВПЗжбЇЩњЕФЦкФЉЪ§бЇГЩМЈЕФжаЮЛЪ§ЪЧ ЃЌ![]() зщЕФЦкФЉЪ§бЇГЩМЈЕФжкЪ§ЪЧ ЃЛ
зщЕФЦкФЉЪ§бЇГЩМЈЕФжкЪ§ЪЧ ЃЛ
ЃЈ3ЃЉетИібЇаЃОХФъМЖЙВгабЇЩњ![]() ШЫЃЌШєЗжЪ§ЮЊ
ШЫЃЌШєЗжЪ§ЮЊ![]() Зж(КЌ
Зж(КЌ![]() Зж)вдЩЯЮЊгХауЃЌЧыЙРМЦетДЮОХФъМЖбЇЩњЦкФЉЪ§бЇПМЪдГЩМЈЮЊгХауЕФбЇЩњШЫЪ§ДѓдМгаЖрЩйЃП
Зж)вдЩЯЮЊгХауЃЌЧыЙРМЦетДЮОХФъМЖбЇЩњЦкФЉЪ§бЇПМЪдГЩМЈЮЊгХауЕФбЇЩњШЫЪ§ДѓдМгаЖрЩйЃП