题目内容
【题目】如图,△ABC中,点D,E分别是边AB,AC上的点,DE∥BC,点H是边BC上的点,连接AH交线段DE于点G,且BH=DE=12,DG=8,S△ADG=12,则S四边形BCED=( )

A.24B.22.5C.20D.25
【答案】B
【解析】
由相似三角形的判定与性质求出BC的长为18,△ADG与△AGE同高不同底求出S△AGE的面积为6,最后根据图形的面积的和差法求出S四边形BCED的面积为22.5.
如图所示:
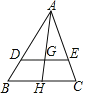
∵DE∥BC,
∴△ADE∽△ABC,
∴![]() ,
,
又∵BH=DE=12,DG=8,
∴![]() ,
,
又∵DE=DG+GE,
∴GE=12﹣8=4,
又∵△ADG与△AGE的高相等,
∴![]() ,
,
又∵S△ADG=12,
∴![]() ,
,
又∵S△ADE=S△ADG+S△AGE,
∴S△ADE=12+6=18,
又∵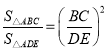 ,
,
∴![]() ,
,
又∵S四边形BCED=S△ABC﹣S△ADE,
∴![]() ,
,
故选:B.

练习册系列答案
相关题目
【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为![]() 分)、
分)、![]() 分)、
分)、![]() 分)、
分)、![]() 分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
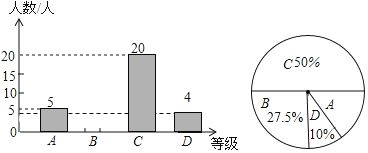
其中组![]() 的期末数学成绩如下
的期末数学成绩如下
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请补全条形统计图;
(2)这部分学生的期末数学成绩的中位数是 ,![]() 组的期末数学成绩的众数是 ;
组的期末数学成绩的众数是 ;
(3)这个学校九年级共有学生![]() 人,若分数为
人,若分数为![]() 分(含
分(含![]() 分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?