题目内容
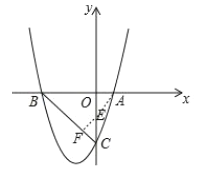
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C(0,3)
与x轴交于A、B两点,与y轴交于点C(0,3)
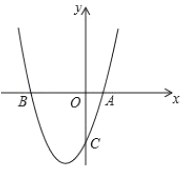
(1)求该抛物线的解析式;
(2)点![]() 为该抛物线上的一点、且在第二象限内,连接
为该抛物线上的一点、且在第二象限内,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若点![]() 为线段
为线段![]() 上一动点,试求
上一动点,试求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)
;(3)![]() .
.
【解析】
(1)把点C(0,3)代入抛物线![]() 即可求出答案;
即可求出答案;
(2)过![]() 点作
点作![]() 轴的垂线,交
轴的垂线,交![]() 轴于点
轴于点![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,利用
,利用![]() 列方程即可求出点
列方程即可求出点![]() 的坐标;
的坐标;
(3)过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() ,可知当
,可知当![]() 、
、![]() 、
、![]() 三点共线时,
三点共线时,![]() 最小,即
最小,即![]() 最小,设直线
最小,设直线![]() 的表达式为:
的表达式为:![]() ,将点
,将点![]() 坐标
坐标![]() 代入求出解析式,并求出
代入求出解析式,并求出![]() 点的坐标,进而可求出
点的坐标,进而可求出![]() 的最小值.
的最小值.
解:(1)把点![]() 的坐标代入抛物线表达式得:
的坐标代入抛物线表达式得:![]() ,
,
解得:![]() ,
,
故该抛物线的解析式为:![]() ;
;
(2)过![]() 点作
点作![]() 轴的垂线,交
轴的垂线,交![]() 轴于点
轴于点![]() ,
,

设:点![]() 的坐标为
的坐标为![]() ,
,
∵![]() ,
,
∴![]() ,
,
即:![]() ,
,![]() ,
,
解得:![]() 或1(舍去
或1(舍去![]() ),
),
故点![]() 的坐标为
的坐标为![]() ;
;
(3)过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,
则![]() ,
,![]() ,
,
∴当![]() 、
、![]() 、
、![]() 三点共线时,
三点共线时,![]() 最小,即
最小,即![]() 最小,
最小,
设:直线![]() 的表达式为:
的表达式为:![]() ,
,
将点![]() 坐标
坐标![]() 代入上式,
代入上式,![]() ,则
,则![]() ,
,
则直线![]() 的表达式为:
的表达式为:![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,![]()
![]() .
.

练习册系列答案
相关题目