Question

【题目】正方形ABCD与正方形OEFG中，点D和点F的坐标分别为（﹣3，2）和（1，﹣1），则这两个正方形的位似中心的坐标为________．

Answer 1

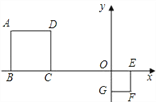
【答案】（﹣1，0）或（5，﹣2）

【解析】试题分析：由图形可得两个位似图形的位似中心必在x轴上，连接AF、DG，其交点即为位似中心，进而再由位似比即可求解位似中心的坐标．

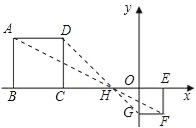
解：当位似中心在两正方形之间，

连接AF、DG，交于H，如图所示，则点H为其位似中心，且H在x轴上，

∵点D的纵坐标为2，点F的纵坐标为1，

∴其位似比为2：1，

∴CH=2HO，即OH=OC，

又C（﹣3，0），∴OC=3，

∴OH=1，

所以其位似中心的坐标为（﹣1，0）；

当位似中心在正方形OEFG的右侧时，如图所示，连接DE并延长，连接CF并延长，

两延长线交于M，过M作MN⊥x轴，

∵点D的纵坐标为2，点F的纵坐标为1，

∴其位似比为2：1，

∴EF=DC，即EF为△MDC的中位线，

∴ME=DE，又∠DEC=∠MEN，∠DCE=∠MNE=90°，

∴△DCE≌△MNE，

∴CE=EN=OC+OE=3+1=4，即ON=5，MN=DC=2，

则M坐标为（5，﹣2），

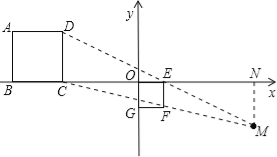
综上，位似中心为：（﹣1，0）或（5，﹣2）．

故答案为：（﹣1，0）或（5，﹣2）．