题目内容
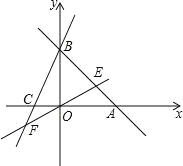
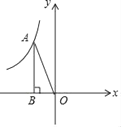
【题目】如图，在平面直角坐标系xOy中，反比例函数y＝﹣
在第二象限的图象上有一点A，过点A作AB⊥x轴于点B，则S△AOB＝_____．
【答案】2
【解析】
设出A的坐标为（a，b），根据A为第二象限的点，得到a小于0，b大于0，进而表示出AB及OB的长，再由A为反比例函数图象上，将A坐标代入反比例函数解析式中，得到-ab=4，最后由三角形AOB为直角三角形，利用两直角边乘积的一半表示出三角形AOB的面积，将-ab=4代入，即可求出三角形AOB的面积．
解：设A的坐标为（a，b）（a＜0，b＞0），
则OB=-a，AB=b，
又∵A在反比例函数y=-
图象上，
∴将x=a，y=b代入反比例函数解析式得：b=-
，即-ab=4，
又∵△AOB为直角三角形，
∴S△AOB=
OBAB=-ab=2．
故答案为：2．
练习册系列答案
相关题目
【题目】行驶中的汽车，在刹车后由于惯性的原因，还要继续向前滑行一段距离才能停住，这段距离称为“刹车距离”．为了测定某种型号汽车的刹车性能，对这种汽车的刹车距离进行测试，测得的数据如下表：
刹车时车速(千米/时) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
刹车距离(米) | 0 | 0.1 | 0.3 | 0.6 | 1 | 1.6 | 2.1 |
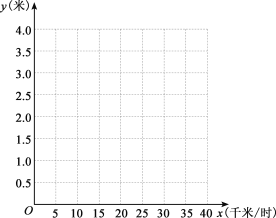
（1）在如图所示的直角坐标系中，以刹车时车速为横坐标，以刹车距离为纵坐标，描出这些数据所表示的点，并用平滑的曲线连结这些点，得到某函数的大致图象；
（2）测量必然存在误差，通过观察图象估计函数的类型，求出一个大致满足这些数据的函数表达式；
（3）一辆该型号汽车在高速公路上发生交通事故，现场测得刹车距离约为40米，已知这条高速公路限速100千米/时，请根据你确定的函数表达式，通过计算判断在事故发生时，汽车是否超速行驶．
