题目内容
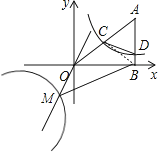
【题目】如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支经过AO的中点C,且与AB交于点D.
的图象的一支经过AO的中点C,且与AB交于点D.
(1)求反比例函数解析式
(2)若函数y=3x与y=![]() 的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比
的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比
【答案】
(1)
解:∵A点的坐标为(8,y),
∴OB=8,
∵AB⊥x轴于点B,sin∠OAB=![]() ,
,
∴![]() =
=![]() ,
,
∴OA=10,
由勾股定理得:AB=![]() =6,
=6,
∵点C是OA的中点,且在第一象限内,
∴C(4,3),
∵点C在反比例函数y=![]() 的图象上,
的图象上,
∴k=12,
∴反比例函数解析式为:y=![]() ;
;
(2)
解:将y=3x与y=![]() 联立成方程组,得:
联立成方程组,得:
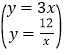 ,
,
解得:![]() ,
,![]() ,
,
∵M是直线与双曲线另一支的交点,
∴M(﹣2,﹣6),
∵点D在AB上,
∴点D的横坐标为8,
∵点D在反比例函数y=![]() 的图象上,
的图象上,
∴点D的纵坐标为![]() ,
,
∴D(8,![]() ),
),
∴BD=![]() ,
,
连接BC,如图所示,
∵S△MOB=![]() 8|﹣6|=24,
8|﹣6|=24,
S四边形OCDB=S△OBC+S△BCD=![]() 83+
83+![]()
![]() 4=15,
4=15,
∴![]() .
.
【解析】(1)先根据锐角三角函数的定义,求出OA的值,然后根据勾股定理求出AB的值,然后由C点是OA的中点,求出C点的坐标,然后将C的坐标代入反比例函数y=![]() 中,即可确定反比例函数解析式;
中,即可确定反比例函数解析式;
(2)先将y=3x与y=![]() 联立成方程组,求出点M的坐标,然后求出点D的坐标,然后连接BC,分别求出△OMB的面积,△OBC的面积,△BCD的面积,进而确定四边形OCDB的面积,进而可求三角形OMB与四边形OCDB的面积的比.
联立成方程组,求出点M的坐标,然后求出点D的坐标,然后连接BC,分别求出△OMB的面积,△OBC的面积,△BCD的面积,进而确定四边形OCDB的面积,进而可求三角形OMB与四边形OCDB的面积的比.

【题目】甲,乙两人是NBA联盟凯尔特人队的两位明星球员,两人在前五个赛季的罚球
命中率如下表所示:
甲球员的命中率(%) | 87 | 86 | 83 | 85 | 79 |
乙球员的命中率(%) | 87 | 85 | 84 | 80 | 84 |
(1)分别求出甲,乙两位球员在前五个赛季罚球的平均命中率;
(2)在某场比赛中,因对方球员技术犯规需要凯尔特人队选派一名队员进行罚球,你认为甲,乙两位球员谁来罚球更好?(请通过计算说明理由)