题目内容
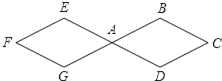
【题目】如图,将等边△ABC绕点C顺时针旋转120得到 ![]() EDC,连接AD,BD.
EDC,连接AD,BD.
则下列结论:
①AC=AD;
②BD ![]() AC;
AC;
③四边形ACED是菱形.
其中正确的个数是( )
A.O
B.1
C.2
D.3
【答案】D
【解析】解 ;∵等边△ABC绕点C顺时针旋转120°得到△EDC,
∴∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,
∴∠ACD=120°-60°=60°.
∴△ACD是等边三角形.
∴AC=AD,AC=AD=DE=CE. 故①符合题意;
∴四边形ACED是菱形,故③符合题意;
∵等边△ABC绕点C顺时针旋转120°得到△EDC,AC=AD,
∴AB=BC=CD=AD.
∴四边形ABCD是菱形,
∴BD⊥AC,故②符合题意
故应选 :D.
根据旋转的性质,旋转前后的对应边和对应角相等,结合等边三角形的判定,即可得到△ACD是等边三角形,从而判断①的正误;
然后依据菱形的判定定理,四条边均相等的四边形为菱形,即可判断③的正误.再根据菱形的性质对角线互相垂直即可判断出②正确。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目