题目内容
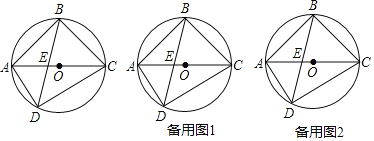
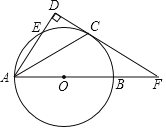
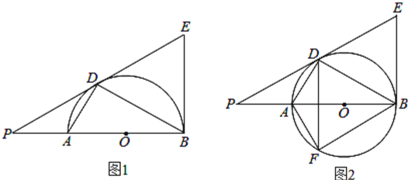
【题目】如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD交圆的切线BE于点E.
(1)证明:直线PD是⊙O的切线;
(2)如果∠BED=60°,PD=![]() ,求PA的长;
,求PA的长;
(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.
【答案】(1)见解析;(2)1;(3)见解析
【解析】
(1)连接OD,由AB是圆O的直径可得∠ADB=90°,再利用角度的相互转换求得∠ADO+∠PDA=90°,即可得出直线PD为⊙O的切线;
(2)求出∠P=30°,解直角三角形求出OD,结合勾股定理可得出PO,最后根据PA=PO-AO可得出结果;
(3)根据折叠和已知求出∠P=∠PBF,根据平行线的判定推出DE∥BF,求出DF⊥AB,BE⊥AB,推出DF∥BE,求出ED=EB,根据菱形的判定推出即可.
(1)证明:如图1,连接OD,

∵AB是圆O的直径,∴∠ADB=90°,
∴∠ADO+∠BDO=90°,
又∵DO=BO,∴∠BDO=∠PBD,
∵∠PDA=∠PBD,∴∠BDO=∠PDA,
∴∠ADO+∠PDA=90°,即PD⊥OD,
∵点D在⊙O上,
∴直线PD为⊙O的切线.
(2)解:∵BE是⊙O的切线,∴∠EBA=90°,
∵∠BED=60°,∴∠P=30°,
∵PD为⊙O的切线,∴∠PDO=90°,
在Rt△PDO中,∠P=30°,PD=![]() ,
,
∴![]() ,解得OD=1,
,解得OD=1,
∴![]() ,
,
∴PA=PO﹣AO=2﹣1=1.
(3)证明:如图2中,依题意得:∠ADF=∠PDA,∠APD=∠AFD,
∵∠PDA=∠PBD,∠ADF=∠ABF,∠AFD=∠PBD,
∴∠ADF=∠AFD=∠APD=∠ABF,
∴AD=AF,BF∥PD,即BF∥DE.
又∠DAB+∠DBA=90°,∴∠DAB+∠ADF=90°,
∴DF⊥PB.
∵BE为切线,
∴BE⊥PB,
∴DF∥BE,
∴四边形DFBE为平行四边形,
∵PE、BE为切线,
∴BE=DE,
∴四边形DFBE为菱形.

【题目】水果店购进某种水果的成本为10元/千克,经市场调研,获得销售单价p(元/千克)与销售时间t(1≤t≤15,t为整数)(天)之间的部分数据如下表:
销售时间t(1≤t≤15,t为整数)(天) | 1 | 4 | 5 | 8 | 12 |
销售单价p(元/千克) | 20.25 | 21 | 21.25 | 22 | 23 |
已知p与t之间的变化规律符合一次函数关系.
(1)试求p关于t的函数表达式;
(2)若该水果的日销量y(千克)与销售时间t(天)的关系满足一次函数y=-2t+120(1≤t≤15,t为整数).
① 求销售过程中最大日销售利润为多少?
② 在实际销售的前12天中,公司决定每销售1千克水果就捐赠n元利润(n<3)给“精准扶贫”对象.现发现:在前12天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围