题目内容
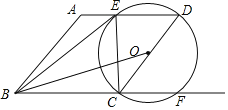
【题目】如图,在菱形ABCD中,取CD中点O,以O为圆心OD为半径作圆交AD于E交BC的延长线交于点F,AB=4,BE=5,连结OB
(1)求DE的长;
(2)求tan∠OBC的值.
【答案】(1)![]() ;(2)
;(2) ![]() .
.
【解析】
(1)根据菱形的性质得到AB=BC=CD=4,AD∥BC,根据圆周角定理得到∠DEC=90°,根据勾股定理即可得到结论;
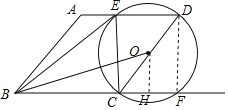
(2)连接DF,过O作OH⊥CF于H,推出四边形ECFD是矩形,得到DF=CE=3,CF=DE=![]() ,根据三角函数的定义即可得到结论.
,根据三角函数的定义即可得到结论.
解:(1)∵四边形ABCD是菱形,
∴AB=BC=CD=4,AD∥BC,
∵CD是⊙O的直径,
∴∠DEC=90°,
∴∠BCE=∠DEC=90°,
∴CE=![]() =3,
=3,
∴DE=![]() ;
;
(2)连接DF,过O作OH⊥CF于H,
∵CD是⊙O的直径,
∴∠DFC=90°,
∴四边形ECFD是矩形,
∴DF=CE=3,CF=DE=![]() ,
,
∴CH=![]() ,
,
∴OH=![]() DF=
DF=![]() ,
,
∴BH=BC+CH=![]() ,
,
∴tan∠OBC=![]() .
.

练习册系列答案
相关题目
【题目】某校积极参与垃圾分类活动,以班级为单位收集可回收的垃圾,下面是七年级各班一周收集的可回收垃圾的质量频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的质量频数表
组别(kg) | 频数 |
4.0~4.5 | 2 |
4.5~5.0 | a |
5.0~5.5 | 3 |
5.5~6.0 | 1 |
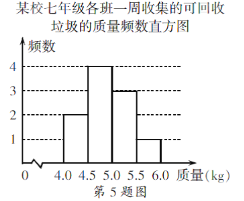
(1)求a的值;
(2)已知收集的可回收垃圾以0.8元/kg被回收,该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元.