题目内容
【题目】如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为 ![]() ,则a的值是( )
,则a的值是( )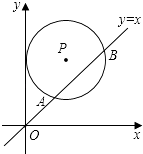
A.2 ![]()
B.2+ ![]()
C.2 ![]()
D.2+ ![]()
【答案】B
【解析】解:过P点作PE⊥AB于E,过P点作PC⊥x轴于C,交AB于D,连接PA.
∵PE⊥AB,AB=2 ![]() ,半径为2,
,半径为2,
∴AE= ![]() AB=
AB= ![]() ,PA=2,
,PA=2,
根据勾股定理得:PE= ![]() =1,
=1,
∵点A在直线y=x上,
∴∠AOC=45°,
∵∠DCO=90°,
∴∠ODC=45°,
∴△OCD是等腰直角三角形,
∴OC=CD=2,
∴∠PDE=∠ODC=45°,
∴∠DPE=∠PDE=45°,
∴DE=PE=1,
∴PD= ![]() .
.
∵⊙P的圆心是(2,a),
∴a=PD+DC=2+ ![]() .
.
故选:B.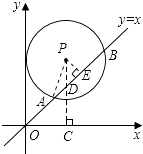
【考点精析】根据题目的已知条件,利用圆的定义和直线与圆的三种位置关系的相关知识可以得到问题的答案,需要掌握平面上到定点的距离等于定长的所有点组成的图形叫做圆.定点称为圆心,定长称为半径;直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.

练习册系列答案
相关题目