题目内容
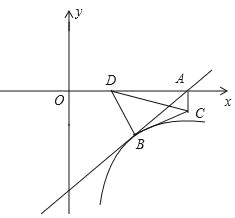
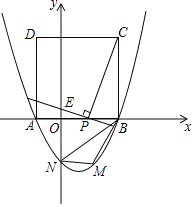
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,以
,以![]() 为边在
为边在![]() 轴上方作正方形
轴上方作正方形![]() ,点
,点![]() 是
是![]() 轴上一动点,连接
轴上一动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线与
的垂线与![]() 轴交于点
轴交于点![]() .
.
(1)求该抛物线的函数关系表达式;
(2)当点![]() 在线段
在线段![]() (点
(点![]() 不与
不与![]() 重合)上运动至何处时,线段
重合)上运动至何处时,线段![]() 的长有最大值?并求出这个最大值;
的长有最大值?并求出这个最大值;
(3)在第四象限的抛物线上任取一点![]() ,连接
,连接![]() .请问:
.请问:![]() 的面积是否存在最大值?若存在,求出此时点
的面积是否存在最大值?若存在,求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 时,线段
时,线段![]() 有最大值.最大值是
有最大值.最大值是![]() ;(3)
;(3)![]() 时,
时,![]() 的面积有最大值,最大值是
的面积有最大值,最大值是![]() ,此时
,此时![]() 点的坐标为
点的坐标为![]() .
.
【解析】
(1)将点![]() 的坐标代入二次函数表达式,即可求解;
的坐标代入二次函数表达式,即可求解;
(2)设![]() ,则
,则![]() ,由
,由![]() 得出比例线段,可表示
得出比例线段,可表示![]() 的长,利用二次函数的性质可求出线段
的长,利用二次函数的性质可求出线段![]() 的最大值;
的最大值;
(3)过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,由
,由![]() 即可求解.
即可求解.
解:(1))∵抛物线![]() 经过
经过![]() ,
,![]() ,
,
把![]() 两点坐标代入上式,
两点坐标代入上式,![]() ,
,
解得:![]() ,
,
故抛物线函数关系表达式为![]() ;
;
(2)∵![]() ,点
,点![]() ,
,
∴![]() ,
,
∵正方形![]() 中,
中,![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 时,线段
时,线段![]() 长有最大值,最大值为
长有最大值,最大值为![]() .
.
即![]() 时,线段
时,线段![]() 有最大值.最大值是
有最大值.最大值是![]() .
.
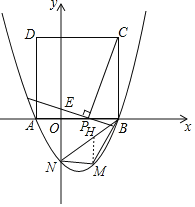
(3)存在.
如图,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,
,
∵抛物线的解析式为![]() ,
,
∴![]() ,
,
∴![]() 点坐标为
点坐标为![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 时,
时,![]() 的面积有最大值,最大值是
的面积有最大值,最大值是![]() ,此时
,此时![]() 点的坐标为
点的坐标为![]() .
.

练习册系列答案
相关题目
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本);并求出售价为多少元时获得最大利润,最大利润是多少?