��Ŀ����
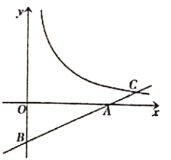
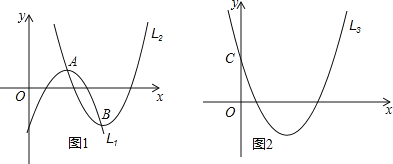
����Ŀ����ͼ1����������L1�Ķ���A��������L2�ϣ�������L2�Ķ���BҲ��������L1�ϣ���A���B���غϣ����ǰ���������������L1��L2����Ϊ���Ѻ��������ߣ��ɼ�һ�������ߵ����Ѻ��������߿����кܶ�����
��1����ͼ2����֪������L3��y=2x2-8x+4��y�ύ�ڵ�C���������C���ڸ������߶Գ���ԳƵĶԳƵ�D�����ꣻ
��2��������Ե�DΪ�����L3�����Ѻ���������L4�Ľ���ʽ����ָ��L3��L4��yͬʱ��x�����������Ա�����ȡֵ��Χ��
��3��������y=a1��x-m��2+n������һ�����Ѻ��������ߵĽ���ʽΪy=a2��x-h��2+k����д��a1��a2�Ĺ�ϵʽ����˵�����ɣ�
���𰸡���1����4��4������2��2��x��4����3��a1=-a2���������£�������
��������
��1����x��0�����y��ֵ�����ɵõ�C�����꣬��������L3��y��2x28x��4�䷽���ɵõ������ߵĶԳ��ᣬ�ɴ˿������C���ڸ������߶Գ���ԳƵĶԳƵ�D�����ꣻ
��2���ɣ�1����֪��D������Ϊ��4��4�������������Ե�DΪ�����L3�����Ѻ���������L4�Ľ���ʽ�������L4�Ľ���ʽ�����������L3��L4��yͬʱ��x�����������Ա�����ȡֵ��Χ��
��3�����ݣ�������L1�Ķ���A��������L2�ϣ�������L2�Ķ���BҲ��������L1�ϣ������г��������̣���ӿɵã���a1��a2����mh��2��0���ɵ�a1��a2.
�⣺��1����������L3��y=2x2-8x+4��
��y=2��x-2��2-4��
�ඥ��Ϊ��2��4�����Գ���Ϊx=2��
��x=0����y=4��
��C��0��4����
���C���ڸ������߶Գ���ԳƵĶԳƵ�D������Ϊ����4��4����
��2�����Ե�D��4��4��Ϊ�����������L4���㣨2��-4����
��L4�Ľ���ʽ![]() ��
��
���㣨2��-4������L4�ɵã�a=-2��
��L4�Ľ���ʽΪy=-2��x-4��2+4��
L3��L4����������ֱ�Ϊ��4��4���ͣ�2��-4��
��L3��L4��yͬʱ��x�����������Ա�����ȡֵ��Χ�ǣ�2��x��4ʱ��
��3��a1=-a2��
�������£�
��������L1�Ķ���A��������L2�ϣ�������L2�Ķ���BҲ��������L1�ϣ�
��������������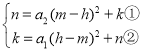 ��
��
��+�ڵã���a1+a2����m-h��2=0��
��a1=-a2��