Question

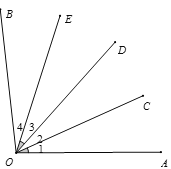
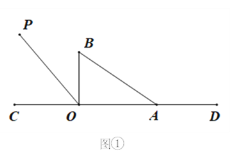
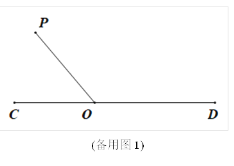
【题目】如图①，直线CD上有一点O，过点O在直线CD上方作射线OP．将一直角三角尺AOB（∠AOB=90°）的直角顶点放在点O处，一条直角边OA在射线OD上，另一边OB在直线CD上方．将直角三角板绕着点O逆时针旋转．

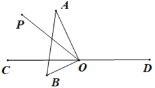
(1)当直角三角板旋转到如图②的位置，OB恰好平分∠COP时，试证明：OA边恰好平分∠POD.

(2)若射线OP的位置保持不变，且∠COP=50°．当直角三角尺旋转到边AB与射线OC相交时则∠BOC与∠AOP有怎样的数量关系?试画出图形，写出数量关系，并写出说理过程.

Answer 1

【答案】(1)见解析;(2)见解析.

【解析】

（1）根据角平分线的定义得到∠BOC=∠BOP ，再根据余角的定义可得∠AOD=∠AOP，根据角平分线的定义即可得到结论；
（2）分情况讨论：①当OA在∠POD内部或与OP重合,OB在CD下方时，②当OA在∠POC内部,OB在CD下方.

（1）∵OB恰好平分∠COP

∴∠BOC=∠BOP

又∵∠AOB＝90°

∴∠AOD＝180°－∠AOB－∠BOC

＝180°－90°－∠BOC＝90°－∠BOC

∠AOP＝∠AOB－∠BOP＝90°－∠BOP＝90°－∠BOC

∴∠AOD=∠AOP

∴OA平分∠POD

(2)①如图，当OA在∠POD内部或与OP重合,OB在CD下方时，

∠AOP＋∠BOC＝40

理由：∵∠AOB＝90°,∠COP=50°

∴∠AOP＋∠BOC＝90°－∠POC＝40°．

即：∠AOP＋∠BOC＝40°

②如图，当OA在∠POC内部,OB在CD下方时，

∠BOC－∠AOP＝40°

理由：∵∠AOC＝∠POC－∠AOP＝50°－∠AOP

∠AOC＝∠AOB－∠BOC＝90°－∠BOC

∴50°－∠AOP＝90°－∠BOC

∴∠BOC－∠AOP＝40°

综上所述，当OA在∠POD内部或与OP重合,OB在CD下方时，

∠AOP＋∠BOC＝40°；当OA在∠POC内部,OB在CD下方时，

∠BOC－∠AOP＝40°.