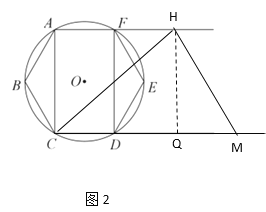
题目内容
【题目】已知多边形![]() 是
是![]() 的内接正六边形,联结
的内接正六边形,联结![]() 、
、![]() ,点
,点![]() 是射线
是射线![]() 上的一个动点,联结
上的一个动点,联结![]() ,直线
,直线![]() 交射线
交射线![]() 于点
于点![]() ,作
,作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,设
,设![]() 的半径为
的半径为![]() .
.
(1)求证:四边形![]() 是矩形.
是矩形.
(2)当![]() 经过点
经过点![]() 时,
时,![]() 与
与![]() 外切,求
外切,求![]() 的半径(用
的半径(用![]() 的代数式表示).
的代数式表示).
(3)当![]() ,求点
,求点![]() 、
、![]() 、
、![]() 、
、![]() 构成的四边形的面积(用
构成的四边形的面积(用![]() 及含
及含![]() 的三角比的式子表示).
的三角比的式子表示).


【答案】(1)证明详见解析;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据正多边形的性质和矩形的判定解答即可;
(2)连接OC、OD,证明△OCD是等边三角形得到CD=OC=r,∠OCD=60°,作ON⊥CD求出ON=![]() ,由四边形ACDF是矩形得到∠AHC=∠ECD=30°,由此得到CH=2AC=
,由四边形ACDF是矩形得到∠AHC=∠ECD=30°,由此得到CH=2AC=![]() ,由cos∠HCM=
,由cos∠HCM=![]() ,得CM=4r,MN=
,得CM=4r,MN=![]() ,利用勾股定理求出OM=
,利用勾股定理求出OM=![]() ,依据
,依据![]() 与
与![]() 外切即可得到答案;
外切即可得到答案;
(3)作HQ⊥CM于Q,由![]() ,MH⊥CH可得∠QHM=
,MH⊥CH可得∠QHM=![]() ,再由AF∥CD,AC⊥CD知HQ=AC=
,再由AF∥CD,AC⊥CD知HQ=AC=![]() ,继而求得CQ=
,继而求得CQ=![]() ,MQ=
,MQ=![]() ,则CM=
,则CM=![]() ,再分
,再分![]() 、
、![]() 、
、![]() 三种情况分别求解即可.
三种情况分别求解即可.
(1)∵多边形![]() 是
是![]() 的内接正六边形,
的内接正六边形,
∴AB=AC,∠ABC=∠BAF=![]() ,
,
∴∠BAC=∠BCA,
∵∠BAC+∠BCA+∠ABC=180°
∴∠BAC=30°,
∴∠CAF=90°,
同理∠ACD=90°,∠AFD=90°,
∴四边形ACDF是矩形;
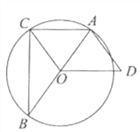
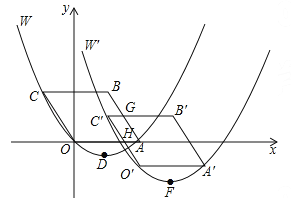
(2)如图1,连接OC、OD,
由题意得:OC=OD,![]()
∴△OCD是等边三角形,
作ON⊥CD,垂足为N,
∴ CN=![]() CD=
CD=![]() r,由
r,由![]() 得
得![]() ,
,
作OP⊥AC于点P,
∴CP=![]() AC,
AC,
∵∠OCP=90°-60°=30°
∴CP=![]() ,
,
∴AC=![]() ,
,
当CH经过点E时,可知∠ECD=30°
∵四边形ACDF是矩形,
∴AF∥CD
∴∠AHC=∠ECD=30°,
在Rt△ACH中,CH=2AC=![]() ,
,
∵MH⊥CH,
∴cos∠HCM=![]() ,得CM=4r
,得CM=4r
∴MN=![]() ,
,
在Rt△MON中,OM=![]() =
=![]() ,
,
∵![]() 与
与![]() 外切,
外切,
∴![]() ,即
,即![]() 的半径为
的半径为![]() ,
,
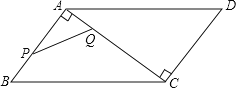
(3)如图2,
作HQ⊥CM于Q,
由![]() ,MH⊥CH可得∠QHM=
,MH⊥CH可得∠QHM=![]()
∵AF∥CD,AC⊥CD
∴HQ=AC=![]()
∴![]() ,
, ![]()
∴CM=![]() ,
,
①当![]() 时,点H在边AF的延长线上,此时点C、M、H、F构成的四边形为梯形,
时,点H在边AF的延长线上,此时点C、M、H、F构成的四边形为梯形,
∵FH=DQ=CQ-CD=![]() ,
,
∴S=![]() ;
;
②当![]() 时,点H与点F重合,此时点C、M、H、F构成三角形,非四边形,所以舍去;
时,点H与点F重合,此时点C、M、H、F构成三角形,非四边形,所以舍去;
③![]() 时,点H在边AF上,此时点C、M、H、F构成的四边形为梯形,
时,点H在边AF上,此时点C、M、H、F构成的四边形为梯形,
∵FH=DQ=CD-CQ=![]() ,
,
∴S=![]()
![]()
综上,点![]() 、
、![]() 、
、![]() 、
、![]() 构成的四边形的面积
构成的四边形的面积![]() 或
或![]() .
.