题目内容
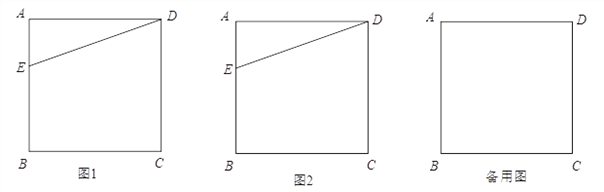
【题目】如图,在正方形ABCD中,E为AB边上一点,连接DE,将△ADE绕点D逆时针旋转90°得到△CDF,作点F关于CD的对称点,记为点G,连接DG.
(1)依题意在图1中补全图形;
(2)连接BD,EG,判断BD与EG的位置关系并在图2中加以证明;
(3)当点E为线段AB的中点时,直接写出∠EDG的正切值.
【答案】(1)补图见解析;(2)BD⊥EG.证明见解析;(3)![]()
【解析】(1)由已知条件补全图形即可;(2)画出图形后利用旋转的性质即可证出BD⊥EG于M;(3)当点E为线段AB的中点时直接写出∠EDG的正切值即可.
解:(1)依题意补全图形如图1:
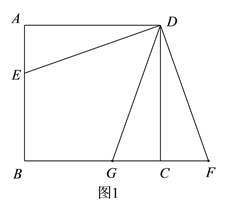
(2)判断: BD⊥EG.
证明:如图2,BD,EG交于M,
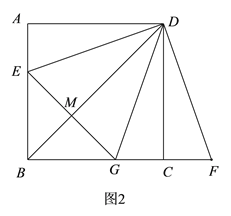
∵正方形ABCD,∴AB=BC,∠DAE=∠DCB =90°
由旋转可得△ADE≌△CDF,DE=DF,AE=CF
∴∠DCF = ∠DAE =∠DCB =90° ∴点B,C,F在一条直线上.
∵点G与点F关于CD的对称
∴△DCG≌△DCF,DG=DF,CG=CF
∴DE=DG,AE=CG
∴BE=BG
∴BD⊥EG于M.
(3)∠EDG的正切值为![]() .
.

练习册系列答案
相关题目