题目内容
8、如图，PA、PB、DE分别切⊙O于A、B、C点，若圆O的半径为6，OP=10，则△PDE的周长为（ ）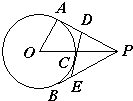
分析：根据切线的性质，得到直角三角形OAP，根据勾股定理求得PA的长；根据切线长定理，得AD=CD，CE=BE，PA=PB，从而求解．
解答：解：∵PA、PB、DE分别切⊙O于A、B、C点，
∴AD=CD，CE=BE，PA=PB，OA⊥AP．
在直角三角形OAP中，根据勾股定理，得AP=8，
∴△PDE的周长为2AP=16．
故选C．
∴AD=CD，CE=BE，PA=PB，OA⊥AP．
在直角三角形OAP中，根据勾股定理，得AP=8，
∴△PDE的周长为2AP=16．
故选C．
点评：此题综合运用了切线长定理和勾股定理．
练习册系列答案
相关题目
如图，PA、PB是⊙O的切线，切点分别为A、B，点C在⊙O上，如果∠P=50°，那么∠ACB等于
6、如图，PA、PB分别切⊙O于点A、B，M是劣弧AB上的一个动点（点A、B除外），过M作⊙O的切线分别交PA、PB于点C、D．设CM的长为x，△PCD的周长为y，在下列图象中，大致表示y与x之间的函数关系的是（ ）
如图，PA、PB分别切⊙0于A、B，PA、BO的延长线交于点Q，连AB，若sin∠AQO=
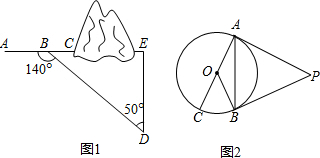
如图，PA、PB是⊙O的切线，切点分别为A、B，若∠APB=40°，则∠ACB=