题目内容
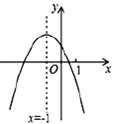
【题目】二次函数![]() 的图像如图,下列结论:①
的图像如图,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .正确的个数为( )
.正确的个数为( )
A. 1个B. 2个C. 3个D. 4个
【答案】D
【解析】
由抛物线的开口方向,抛物线与y轴交点的位置、对称轴即可确定a、b、c的符号,即可对①进行判断;由抛物线与x轴有两个交点判断②即可;由抛物线的对称轴为直线x=-1,可得a=![]() ,当x=1时,y=a+b+c<0,把a=
,当x=1时,y=a+b+c<0,把a=![]() 代入即可对③进行判断;把x=-1代入方程即可求得相应的y的符号,可对④进行判断;综上即可得答案.
代入即可对③进行判断;把x=-1代入方程即可求得相应的y的符号,可对④进行判断;综上即可得答案.
∵抛物线开口向下,与y轴交于正半轴,
∴a<0,c>0,
∵对称轴为直线x=![]() =-1,
=-1,
∴b<0,
∴abc>0,故①正确,
∵抛物线与x轴有两个交点,
∴b2-4ac>0,即4ac-b2<0,故②正确,
∵![]() =-1,
=-1,
∴a=![]() ,
,
∵x=1时,a+b+c<0,
∴![]() +b+c<0,即3b+2c<0,故③正确,
+b+c<0,即3b+2c<0,故③正确,
当x=-1时,a-b+c>0,故④正确,
综上所述:正确的结论有①②③④共4个,
故选D.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目